3.4 Преобразование Фурье в оптической схеме с линзой.

Рассмотрим оптическую схему, изображенную на рис.3.4. Плоский транспарант расположен в плоскости ₁. Комплексная функция пропускания транспаранта . В этой же плоскости расположена тонкая собирающая оптическая линза с фокусным расстоянием, равным f_л. Систему, состоящую из транспаранта и линзы, просвечивают слева в направлении оси 0z плоской оптической волной с амплитудой а₀.

Рис.3.4. Схема расположения транспаранта и линзы.

Плоскость наблюдения оптической волны расположена справа от линзы на расстоянии, равном фокусному расстоянию линзы . Рассмотрим процесс преобразования волны при ее распространении от плоскости до плоскости . Выразим распределение комплексной амплитуды волны непосредственно за плоскостью ₁ (в плоскости, которую обозначим ), после прохождения плоской волны через транспарант и линзу. Для этого помножим функцию распределения волны на входе системы на функцию передачи транспаранта и функцию пропускания плоской линзы:

(3.28)

Далее волна распространяется в свободном пространстве до плоскости наблюдения, которая находится на расстоянии . Для расчета поля в плоскости ₂ при заданном распределении амплитуд в плоскости можно воспользоваться формулой дифракционного интеграла при малых углах дифракции (в параксиальном приближении).

Распределение тогда можно выразить:

(3.29)

Интегрирование в формуле (3.29) проводится по апертуре. Однако, учитывая, что за пределами рассматриваемой апертуры поле равно нулю (можно установить непрозрачный экран, окружающий апертуру), можно расширить пределы интегрирования от - до +.

Кроме того, преобразуем подынтегральное выражение, раскрыв квадраты разностей: и . После подстановки этих выражений в формулу (3.29) получим:

(3.30)

Введем некоторые обозначения:

. (3.31)

Углы ₁ и ₂ – между направлением на соответствующие точки с координатами х₂ и у₂ и осью 0z. Соотношения записаны в приближении малых углов .

Заменив 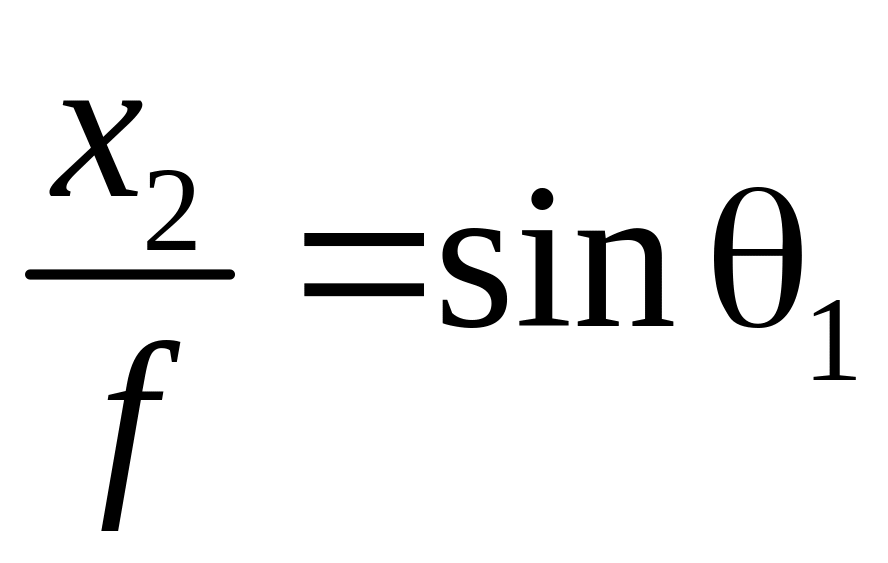и , мы получим:

(3.32)

Как видно формы выражений величин  и  совпадают с формой выражений для пространственных частот, которые мы рассматривали выше, в разделе 1. С учетом (3.32) выражение (3.30) принимает следующий вид:

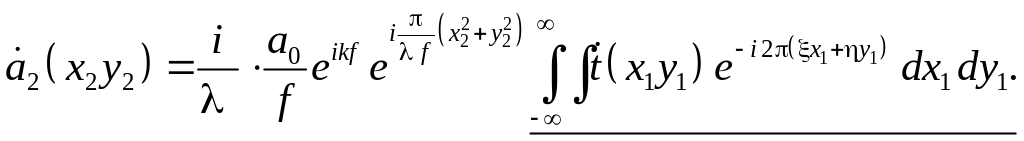(3.33)

Подчеркнутая часть выражения (3.33) является интегралом Фурье. Множитель перед интегралом состоит из постоянного сомножителя, не зависящего от и фазового множителя , отражающего кривизну волнового фронта в плоскости . Если рассматривать распределение интенсивности в плоскости ₂( ), то учитывая, что , все мнимые сомножители перед интегралом при умножении их на комплексно сопряженные величины превратятся в единицы. Тогда распределение плотности мощности в фокусе линзы с точностью до постоянного множителя будет равно квадрату преобразования Фурье от распределения амплитуд в плоскости _1,

3.5. Пространственная фильтрация оптических волн и сигналов.

Поскольку в фокальной плоскости линзы формируется Фурье преобразование исходного распределения волнового фронта, то каждой координате фокальной плоскости линзы соответствует определенная пространственная частота. Если установить в фокальной плоскости непрозрачные экраны в определенных областях, соответствующих некоторым избранным пространственным частотам, то эти пространственные частоты будут исключены из спектра оптического сигнала. После этого скорректированный волновой фронт восстанавливается с помощью второй линзы, фокус которой совмещен с фокусом линзы, выполняющей преобразование Фурье. Таким образом, пространственная фильтрация в оптических схемах основана на замечательном свойстве линзы: она выполняет операцию преобразование Фурье оптического сигнала находящегося перед линзой, при переходе к фокальной плоскости линзы. Следует заметить, что в качестве фильтров в фокальной плоскости могут быть применены не только амплитудные фильтры (диафрагмы, экраны), но также и фазовые фильтры, изменяющие фазовый сдвиг оптической волны на определенных пространственных частотах. Далее рассмотрим некоторые примеры схем пространственной фильтрации.