3.3 Анализ оптической схемы из транспаранта и линзы.

3.3.1.Функция пропускания тонкой линзы. Для анализа нам необходимо будет описать функцию прозрачности линзы, т.е. функцию преобразования волнового фронта при прохождении его через тонкую линзу. С этой целью рассмотрим оптическую схему, изображенную на рис. 3.3.

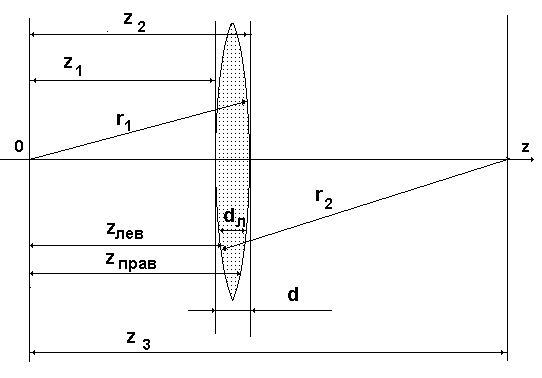
Рис 34.3 Схема для расчета фазовой задержки оптической волны в линзе.

Тонкая линза, изготовленная из прозрачного материала с показателем преломления, равным , окружена воздухом с показателем преломления . Толщина линзы намного меньше, чем радиусы поверхностей r₁ и r₂, образующие линзу. Важное условие состоит в том, что материал линзы прозрачен и не поглощает излучения. При отсутствии поглощения линза представляет собой фазовый транспарант, функцию пропускания которого можно выразить в виде:

(3.16)

Здесь функция отражает зависимость фазовой задержки оптической волны от координат x и y при ее прохождении от плоскости до плоскости (касательных плоскостей к выпуклостям линзы).

Проведем расчет фазовой задержки , которая складывается из фазовой задержки в толще материала линзы c показателем преломления и фазовой задержки в воздушных промежутках между поверхностями, образующими линзу, и плоскостями и . Толщину линзы d_л (х, у) в произвольной точке с координатами х и у найдем рассчитав разность между координатами z правой и левой сферических поверхностей.

d_л ( х , у) = , (3.17)

где

, (3.18)

. (3.19)

Здесь z₃ – координата центра сферы с радиусом r₂ по отношению к точке x=0 расположения центра сферы с радиусом r₁.

Замена квадратного корня его приближенным разложением справедлива в случае параксиального приближения. При этом предполагается,

что . С учетом сделанных приближений толщина материала линзы составит:

d_л (х, у) . (3.20)

Фазовая задержка световой волны с длиной волны  в материале

линзы составит:

. (3.21)

Фазовая задержка в воздушном промежутке между плоскостями и и поверхностями линзы составит:

, (3.22)

где d - расстояние между плоскостями и , а величина - длина воздушного промежутка.

Полный фазовый сдвиг световой волны при ее прохождении от плоскости до плоскости составит:

. (3.23)

Второе слагаемое не зависит от координат х и у и фактически обозначает постоянный, не зависящий от координат фазовый сдвиг при прохождении волны от одной плоскости до другой. Поскольку этот сдвиг равносилен изменению начала отсчета световой волны, он не влияет на функции преобразования волнового фронта в оптической схеме, и его можно отбросить. После этого из формулы (3.23) с учетом (3.20) получим следующую формулу, выражающую зависимость фазового запаздывания волны в тонкой линзе от координат х. и у.

(3.24)

В этом выражении первое слагаемое также представляет постоянный фазовый сдвиг, не зависящий от переменных x, у. Отбросив это слагаемое, получим:

(3.25)

Из геометрической оптики известно соотношение, связывающее

оптическую силу линзы D_л с радиусами сферических поверхностей, образующих линзу.

(3.26)

С учетом выражений (3.25) и (3.26) формулу, характеризующую комплексную функцию пропускания линзы (3.16) можно записать в такой форме:

(3.27)

Следовательно, тонкая линза является фазовым транспарантом, который преобразует волну с плоским фронтом (на входе слева) в волну с волновым фронтом в форме параболоида вращения.