Раздел 4. 24.10.08

Раздел 3.

ДИФРАКЦИОННЫЙ ИНТЕГРАЛ.

Анализ оптичесКОЙсхемы,

состоящей из транспаранта и линзы.

3.1 Дифракционный интеграл, основные положения, формулы.

Дифракционным интегралом называют интегральное преобразование, которое позволяет выразить распределение поля в некоторой области пространства через известное распределение поля на заданной поверхности. В частности, в когерентной оптике дифракционный интеграл применяется для того, чтобы выразить распределение амплитуд поля в плоскости П₂, находящейся на расстоянии от плоскости П₁, через распределение амплитуд поля в первой плоскости П₁, т.е. через распределение поля на излучающей апертуре (рис 3.1).

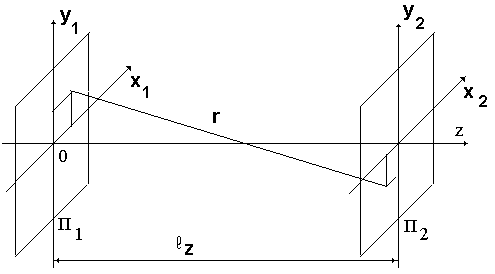
Рис 3.1 Схема, иллюстрирующая расчеты с помощью дифракционного интеграла.

При этом в оптических задачах учитывают ряд обстоятельств, которые значительно упрощают общий вид дифракционного интеграла.

-Излучающую поверхность (апертуру) обычно полагают плоской.

-Принимают во внимание то обстоятельство, что длина волны  оптического излучения очень мала по сравнению с расстоянием r от излучающей апертуры до области наблюдения и учитывают условие Это условие называют оптическим приближением.

-Используют так называемое параксиальное приближение, при котором полагают, что размер апертуры излучения мaл по сравнению с расстоянием между плоскостью апертуры и плоскостью наблюдения.

Дифракционный интеграл в точной формулировке был записан Кирхгофом в 1882 году.¹ Он явился точной формулировкой ранее выдвинутой идеи, называемой принципом Гюйгенса. Эта идея была развита Френелем. Напомним, что согласно принципу Гюйгенса каждая точка волновой поверхности может рассматриваться как самостоятельный точечный источник сферической волны.

С учетом определенных, упомянутых выше приближений, можно записать выражение для искомой функции распределения поля в плоскости П₂ на расстоянии от плоскости П₁ ( , z = 0) через распределение поля в этой плоскости в виде:

, (3.1)

В этой формуле - площадь апертуры, ds – элемент площади dx_1, dy₁, r – текущий радиус вектор между точкой с координатами x_2, y₂ в плоскости П₂ и точкой с координатами x_1,y₁ в плоскости П₁ (рис. 4.1). При условии, что координаты x₁ и y₁, а также x_2, y₂ изменяются лишь в сравнительно небольшой ограниченной области, т.е. и , и аналогично , можно положить, что величина r изменяется очень мало. В этом случае мы не допустим большой ошибки, если положим, что в знаменателе дроби под интегралом в выражении (3.1) заменим переменную величину r на постоянную величину , которая является постоянной, не зависящей от переменных интегрирования. Выведем эту величину за знак интеграла, положив . В то же время следует заметить, что в показателе экспоненты такую замену сделать нельзя.

Величину r в показателе экспоненты представим в виде квадратного корня из суммы квадратов координат, который затем преобразуем с учетом предполагаемой малости отношений и :

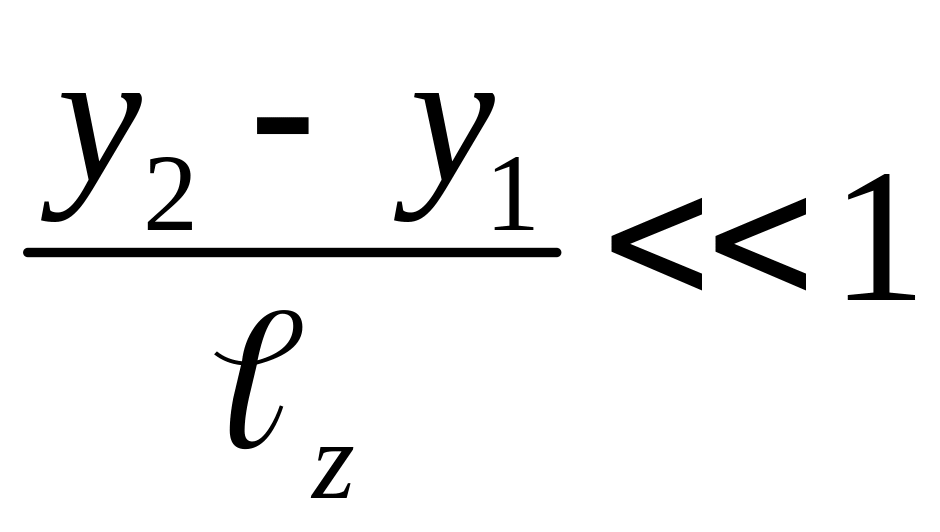. (3.2)

Из (3.1) и (3.2) получим следующее выражение, связывающее распределение комплексных амплитуд поля в плоскости П₂ через распределение комплексных амплитуд в плоскости П₁.

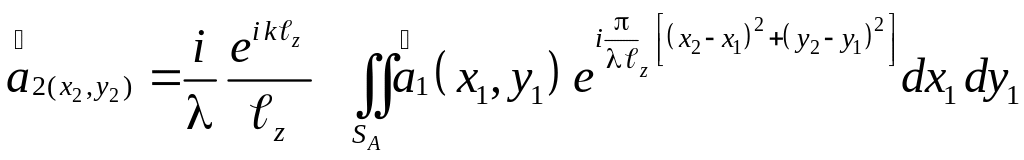. (3.3)

Интересно отметить, что интеграл (3.3) представляет собой свертку функции распределения с функцией вида .

Формула (3.3) содержит в показателе экспоненты квадратичные члены и отражает случай так называемой дифракции Френеля.