30.Эквивалентные схемы замещения четырехполюсников. Передаточная функция.

Эквивалентные схемы замещения четырехполюсников. Любой пассивный четырехполюсник характеризуется тремя независимыми параметрами, поэтому для него можно составить трехэлементную схему замещения — Т-образную или П-образную, которая относительно внешних зажимов будет эквивалентной исходному четырехполюснику (рис.5.2).

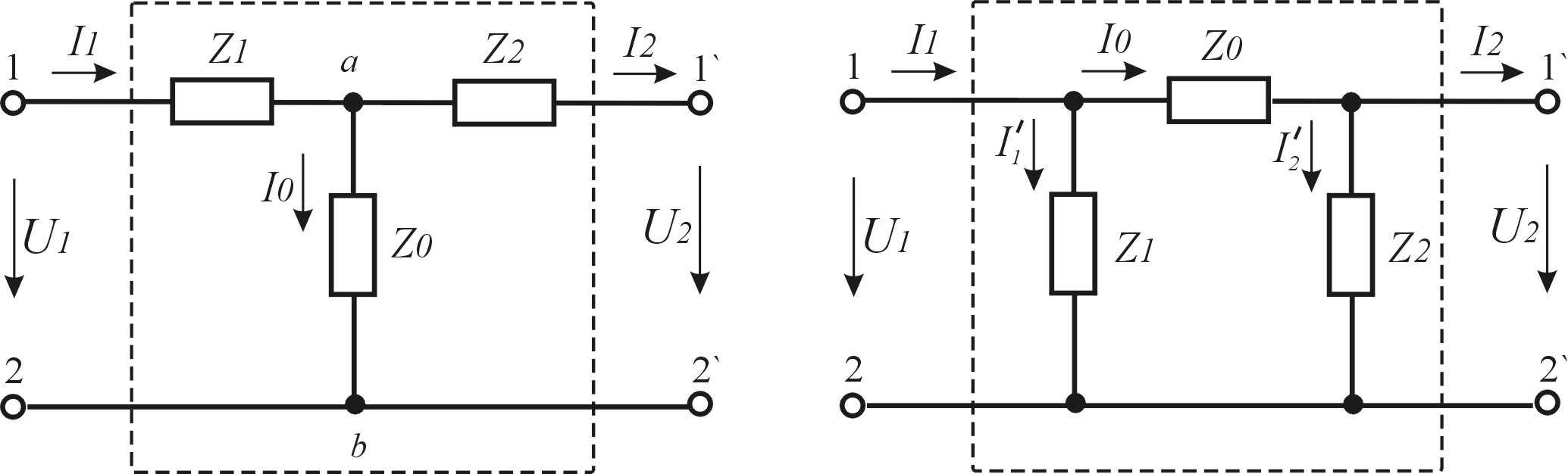
Рисунок 5.2 — Т-образная и П-образная схемы четырехполюсников

Определим для Т-образной схемы замещения связь между входными и выходными величинами токов и напряжений, пользуясь законами Кирхгофа:

;

откуда путем подстановки получаем уравнения в форме А для Т-схемы замещения, которые отображают взаимосвязь между током и напряжением на входе цепи и выходным током и напряжением:

,

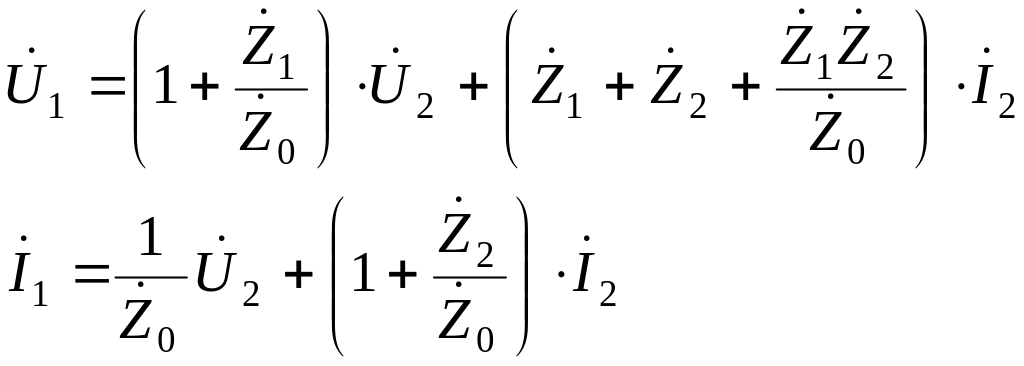где .

Параметры элементов Т-схемы замещения можно определить из полученных коэффициентов следующим образом:

; ; .

Аналогичным образом можно определить коэффициенты и параметры элементов и для П-схемы замещения. Из уравнений

,

получим А-параметры П-схемы замещения

; ; ; ,

и параметры ее элементов: ; ; .

Легко убедиться, что для полученных коэффициентов схем замещения выполняется условие . Таким образом, зная коэффициенты уравнений четырехполюсника произвольной структуры, можно составить для него Т- или П-схему замещения, рассчитав элементы эквивалентной схемы по известным постоянным четырехполюсника.

Передаточная функция. Передаточной функцией (коэффициентом передачи) четырехполюсника называется отношение комплексных амплитуд или комплексов действующих значений электрических величин на выходе и входе четырехполюсника при заданном режиме его работы.

Отношения одноименных электрических величин (коэффициент передачи напряжения) и (коэффициент передачи тока) являются безразмерными величинами (табл.5.1). Отношения разноименных электрических величин (передаточное сопротивление) и (передаточная проводимость) имеют соответственно размерности сопротивления и проводимости.

В общем случае все указанные величины являются комплексными и частотно зависимыми. Зависимость модуля комплексного коэффициента передачи (ККП) от частоты называется амплитудно-частотной характеристикой (АЧХ) четырехполюсника, а зависимость аргумента ККП от частоты представляет ФЧХ.

Запишем ККП по напряжению, используя уравнения воздушного трансформатора (рис.5.5) при холостом ходе на выходных зажимах:

.

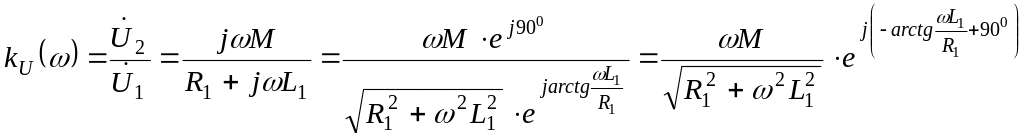Зависимость является АЧХ данного четырехполюсника, а зависимость определяет его ФЧХ.

Зная ККП четырехполюсника, можно вычислить значения выходного тока или напряжения при любом значении частоты входного напряжения.

31.Понятие электрические фильтры. Основные типы пассивных фильтров

Пассивные четырехполюсники — частотные электрические фильтры. Устройства, предназначенные для разделения электрических сигналов разной частоты, называются частотными электрическими фильтрами.

Фильтр пропускает колебания одних частот, а колебания других частот задерживают. При этом пропускание колебаний предполагает их прохождение через фильтр с минимальным затуханием , а задержка колебаний — прохождение колебаний с максимальным затуханием (табл.5.2).

Область частот, в которой фильтр пропускает колебания, называется полосой пропускания фильтра. Область частот, в которой фильтр задерживает сигналы, называется полосой затухания фильтра. Полосу пропускания Т- или П-фильтра (табл.5.2) можно вычислить, используя основное неравенство фильтра

,

где — общее сопротивление последовательного плеча фильтра;

— общая проводимость параллельного плеча фильтра.

В качестве фильтров применяют активные и пассивные четырехполюсники. Фильтры могут содержать различные комбинации соединений резисторов, конденсаторов и катушек индуктивности, а также электронные и полупроводниковые приборы. Далее рассматриваются только идеальные пассивные -фильтры, т.е. фильтры без потерь ( ). На практике в качестве фильтров чаще всего используют симметричные Г-образные, Т-образные, П-образные (табл.5.2) и мостовые фильтры.

Фильтры нижних частот (ФНЧ) имеют полосу пропускания в области частот , а колебания с частотами, более высокими, чем , ФНЧ задерживает.

Фильтры верхних частот (ФВЧ) имеют полосу пропускания в области частот , а колебания с частотами, более низкими, чем , ФВЧ задерживает.

Полосовые фильтры пропускают колебания в некоторой заданной полосе частот , остальные частоты полосовые фильтры задерживают. Полосовые фильтры содержат в последовательных плечах последовательные колебательные контуры, а в параллельных плечах — параллельные колебательные контуры. Границы полосы пропускания этого фильтра будет определяться резонансной частотой , при которой сопротивление последовательных плеч будет минимально, а параллельных — максимально, при этом полоса пропускания определяется из условия .

Заграждающие фильтры задерживают колебания с полосой частот , а в оставшейся части частотного диапазона колебания пропускаются. Полосовые фильтры содержат в последовательных плечах параллельные колебательные контуры, а в параллельных плечах —последовательные колебательные контуры. Полоса пропускания этого фильтра будет определяться резонансной частотой , при которой сопротивление последовательных плеч будет максимально, а параллельных — минимально.