2.2.4 Особенности расчета соединений широких листов

В соединениях широких листов (см. рисунок 2.5) за расчетную нагрузку принимают силу , действующую на фронте одного шага . При этом значение обычно определяют по напряжениям растяжения в сечении листа, не ослабленном отверстиями под заклепки. Напряжение полагают известным из основных расчетов конструкции (расчет прочности стенок котла, резервуара и т. п.):

Прочность листа в сечении, ослабленном отверстиями под заклепки:

Отношение

(2.5)

называют коэффициентом прочности заклепочного шва.

З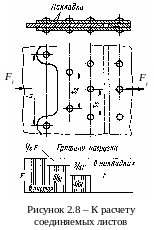 начение показывает, как уменьшается прочность листов при соединении заклепками. Например, для однорядного односрезного шва (рисунок 2.6, а) при стандартных размерах , т.е. образование заклепочного соединения уменьшает прочность листов на 35 %. Понижение прочности деталей – одна из главных отрицательных характеристик заклепочного соединения. Для увеличения значений φ применяют многорядные и многосрезные швы (см. рисунок 2.6, б, в и рисунок 2.7).

На рисунок 2.8 изображена конструкция прочноплотного трехрядного шва с переменным шагом заклепок в рядах (правая половина шва симметрична и на рисунке изображена частично). В этом шве на фронте основного шва расположено шесть заклепок.

Каждая заклепка передает нагрузку, равную 1/6 . В соответствии с этим на рисунке 2.8 даны эпюры продольных сил, возникающих в различных сечениях листов и накладок. Сечение листа по первому ряду заклепок нагружено полной силой . Для того чтобы немного ослабить это сечение, в нем поставлена только одна заклепка (две половины заклепки). Сечение по второму ряду нагружено меньшей силой и, соблюдая условие равнопрочности, в нем можно поставить большее число заклепок и т. д. Малая нагрузка на каждую заклепку, а также две плоскости среза заклепки позволяют значительно уменьшить ее диаметр. Уменьшение диаметра приводит к увеличению коэффициента прочности шва [см. формулу (2.5)], например для рассматриваемого шва . Однако стремление получить высокое значение приводит к сложной и дорогой конструкции соединения.

2.3. Расчет соединений при несимметричном нагружении

Если соединяемые элементы подвержены изгибу (случай несимметричного нагружения), то нагрузка между одиночными заклепочными соединениями распределяется неравномерно. В этом случае расчет групповых соединений сводится обычно к определению наиболее нагруженной заклепки и оценке ее прочности.

Рассмотрим соединение, содержащее заклепок одинакового диаметра d под действием силы F (рисунок 2.9, а). Примем для упрощения, что трение между соединяемыми деталями отсутствует и вся внешняя нагрузка передается через заклепки. Предположим, что деформации (изгиб, сдвиг) соединяемых деталей малы по сравнению с деформациями стержней заклепок. При этих допущениях можно полагать, что возможный взаимный поворот соединяемых деталей (листов) произойдет вокруг точки С (рисунок 2.9, б) – центра масс поперечных сечений стержней заклепок. Следовательно, точку С можно использовать в качестве центра приведения внешней силы.

В результате приведения внецентренной силы F в точку С задача расчета группового соединения сводится к определению наиболее нагруженной заклепки от действия центральной силы F (или ее осевых составляющих) и вращающего момента T=FL (рисунок 2.9, б; L – расстояние от точки С до линии действия силы F).

Если соединение подвержено действию нескольких сил , то в результате приведения их к точке С оно будет нагружено главным вектором и главным моментом от этих сил.

При упругой деформации заклепок действие каждого силового фактора (F и Т) можно рассматривать независимо. Тогда сила, приходящаяся на каждую заклепку от силы F (рисунок 2.9, в), будет равна

где – номер заклепки.

Момент Т вызывает в каждой заклепке реактивную силу, направленную перпендикулярно к радиусу-вектору , проведенному из точки С в центр сечения -й заклепки (рисунок 2.9, г). Эта сила пропорциональна перемещению сечения в результате деформации сдвига. Так как сдвиги сечений заклепок прямо пропорциональны их расстояниям до центра масс, то можно записать