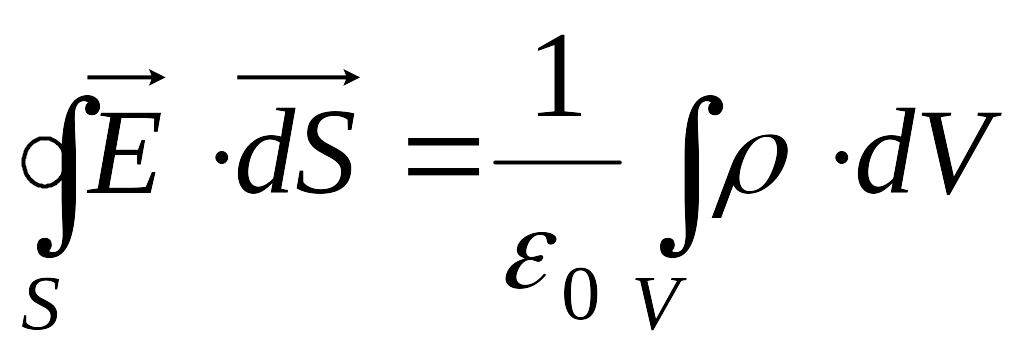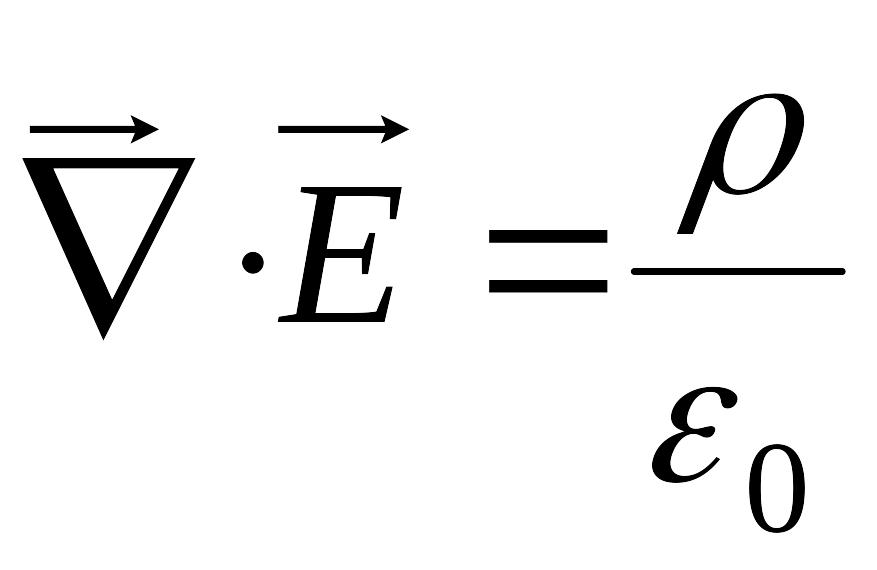§4 Локальна форма теореми про циркуляцію.

За теоремою Стокса:

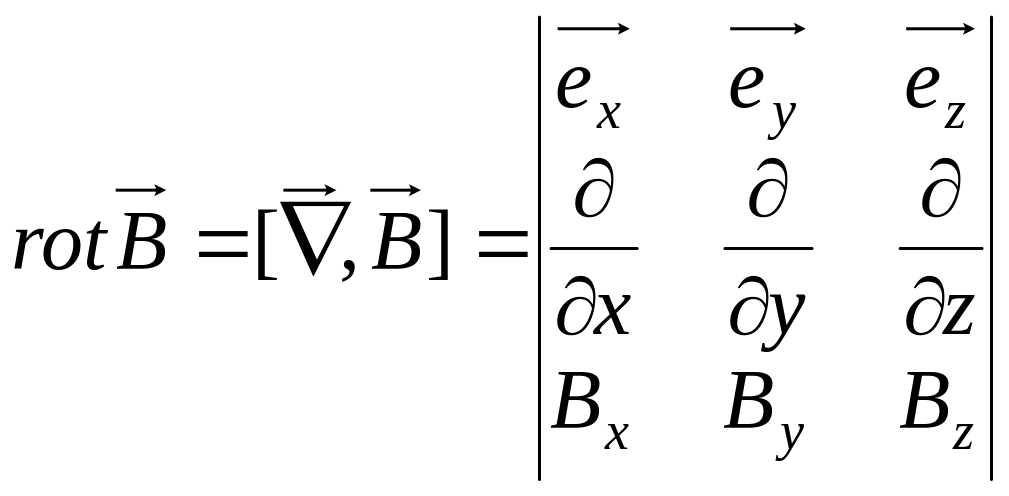
(7.8)

У кожній точці простору в вакуумі ротор магнітного поля дорівнює добутку магнітної сталої на вектор густини струму в цій точці.

§5 Потенціальні та вихрові поля

	Електростатичне поле	Магнітне поле
Силова характеристика
Теорема Гауса в інтегральній формі		поле соленоїдне
Теорема Гауса в локальній формі		поле бездівергентне
Теорема про циркуляцію	поле потенціальне
Теорема про циркуляцію в локальній формі		вихрове поле

Розділ 8. Магнітне поле в речовині. Магнетики.

§ 1. Магнітний момент атомів та молекул. Намагнічування. Вектор .

Атом – мікроскопічний контур з магнітним моментом

І

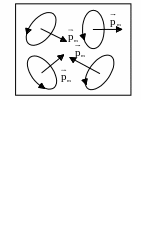
За відсутності зовнішніх полів речовина не проявляє магнітних властивостей, внаслідок теплового руху атомів. При дії магнітного поля виникає сумарний магнітний момент.

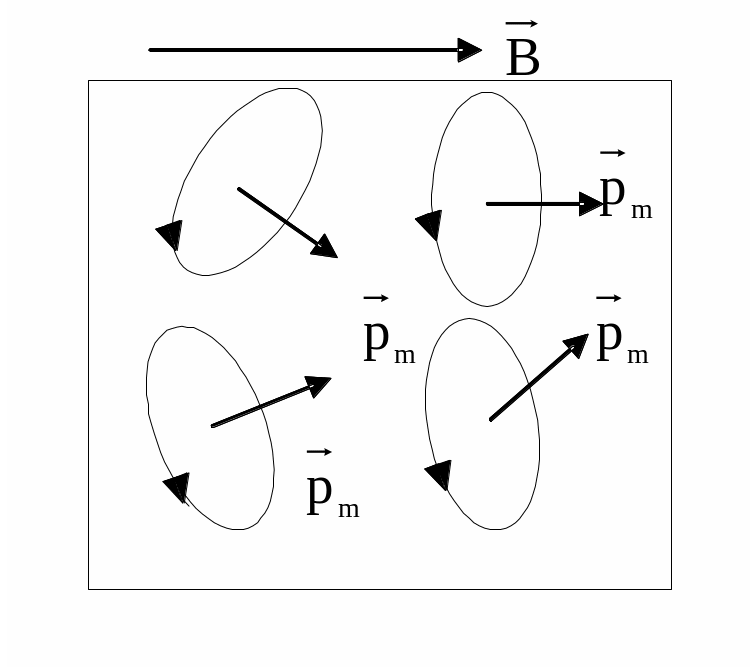
Під дією зовнішнього магнітного поля магнітні моменти набувають переважної орієнтації в напрямку поля, внаслідок чого речовина намагнічується.

Намагнічуванням називається явище виникнення в речовині об’ємного макроскопічного магнітного моменту.

Вектор намагнічування (намагніченість) – сумарний магнітний момент всіх молекул, визначений за фізично нескінченно малим об’ємом взятим в околі точки, що розглядається.

(8.1)

Залежить від:

а) величини магнітного поля в точці;

б) конкретних фізичних властивостей речовини

§2 Струми намагнічування. Теорема Гауса для магнітного поля в речовині.

Намагнічування речовини обумовлене переважною орієнтацією векторів

Те ж саме можна сказати і про елементарні кільцеві струми, пов’язані з кожною молекулою. Їх називають молекулярними струмами.

При намагнічуванні відбувається таке впорядкування руху зарядів в молекулах, в результаті якого по поверхні будь-якого виділеного в намагніченій речовини об’єму циркулює макроскопічний струм, що називається струмом намагнічення.

Струми, що утворюють магнітні моменти і не дають вклад в макроскопічні струми провідності, називаються струмами намагнічування.

- зовнішнє поле в речовині

(8.2)

Теорема Гауса в речовині має такий самий вигляд, як і у вакуумі.

(8.3)

Магнітне поле соленоїдальне.

§ 3. Теорема про циркуляцію магнітного поля в речовині. Вектор напруженості магнітного поля н.

У вакуумі:

Застосовуючи формулу Стокса:

В речовині:

(8.4)

(8.5)

Треба знайти такий допоміжний вектор, ротор якого визначався б лише густиною макроскопічних струмів провідності.

В иберемо всередині речовини довільну поверхню S, яка обмежена контуром l і обчислимо .

В цю суму ненульовий вклад дають струми, які “нанизані”, бо всі інші або не перетинають поверхню, або перетинають її двічі.

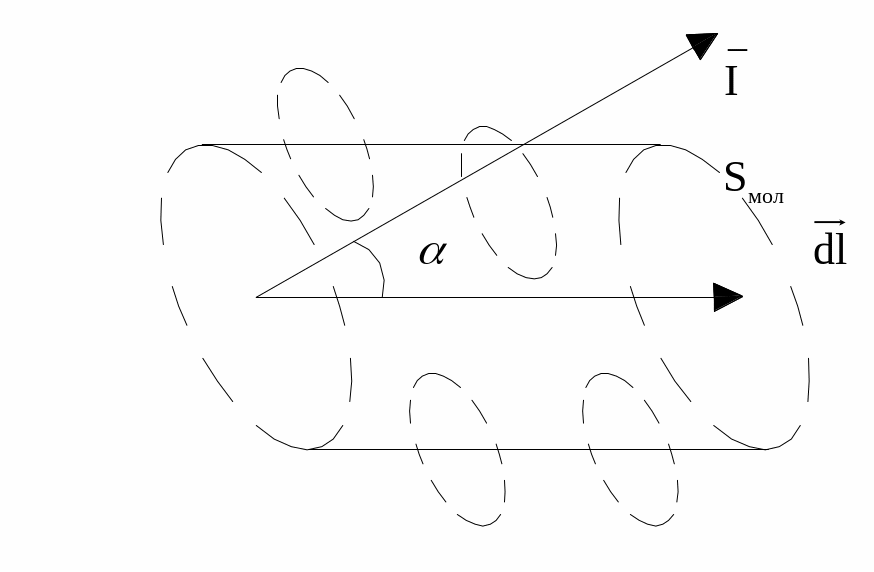
Нанизані на цей контур будуть лише молекулярні струми, центри яких знаходяться всередині циліндра.

Сумарний струм, що охоплюється елементом dl:

-скалярний добуток двох векторів

(8.6)

(8.7)

Якщо в рівнянні (8.5) замінити , то:

(8.8)

У вакуумі:

(8.9)

- локальна форма теореми про циркуляцію вектора .

Ротор вектора напруженості магнітного поля в будь-якій точці магнетика дорівнює густині струмів в цій самій точці.

Проінтегруємо формулу (8.6) за будь-якою поверхнею S:

(8.10)

(8.10) – теорема про циркуляцію магнітного поля в речовині.

(8.10)

Циркуляція вектора напруженості магнітного поля за довільним контуром дорівнює алгебраїчній сумі макроскопічних струмів провідності, що охоплені цим контуром.