§6 Взаємна індукція.

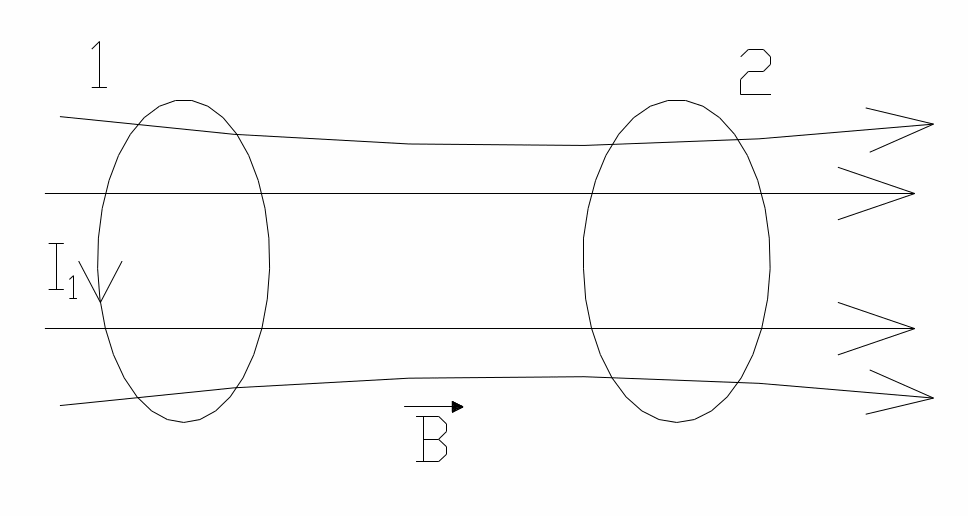
Струм I₁ утворює крізь контур 2 магнітний потік

Якщо , то

(9.11)

– якщо контур жорсткий, а (відсутній феромагнетик).

Якщо , то

(9.12)

Такі 2 контури називають зв’язаними.

Явище виникнення ЕРС в одному з контурів при зміні сили струму в іншому називають взаємною індукцією. Коефіцієнти пропорційності L₁₂ і L₂₁ називають взаємною індуктивністю контурів або коефіцієнтами взаємної індукції.

За відсутності феромагнетика:

Теорема взаємності:

§7 Енергія магнітного поля.

У процесі зміни сили струму в контурі джерело сторонніх ЕРС виконує роботу проти ε_і.

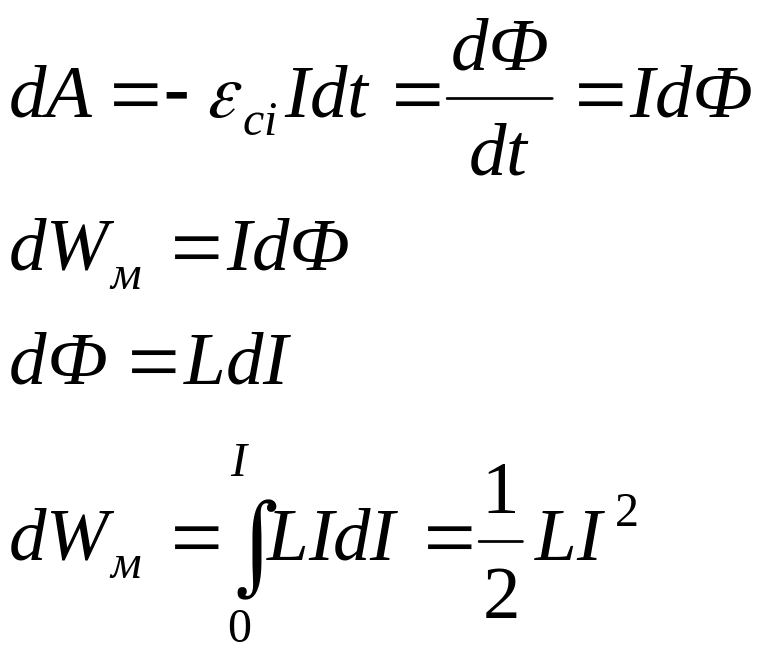
(9.13)

– енергія магнітного поля замкненого провідного контуру зі струмом I i L.

Енергія магнітного поля розподілена в усьому просторі, де локалізоване поле.

Соленоїд зі струмом у вакуумі:

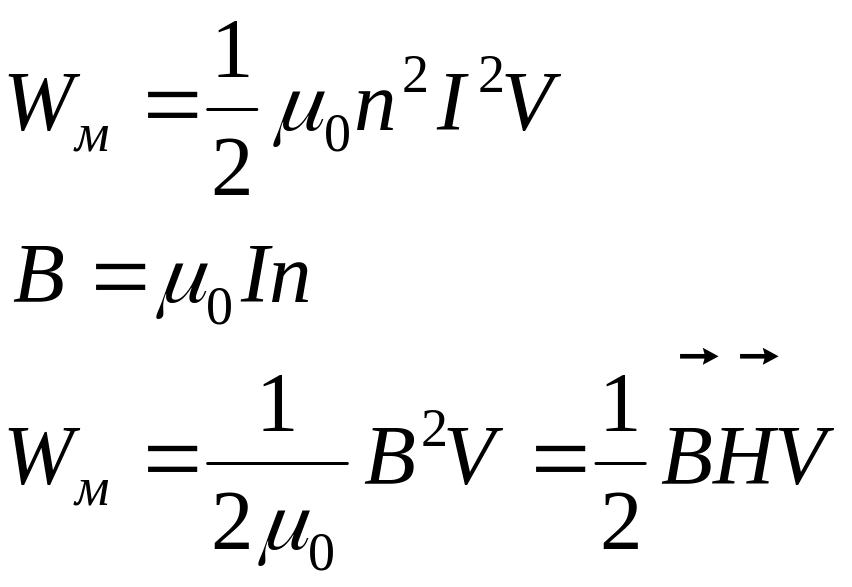
(9.14)

- об’ємна густина енергії магнітного поля в околі кожної точки простору визначається значенням векторів поля в цій точці.

§8 Природа електромагнітної індукції.

1. Виникнення ЕРС самоіндукції в провіднику, що рухається.

- магнітна складова сили Лоренца

В цьому полі напруженість .

Дане поле – непотенціальне, тобто поле сторонніх сил.

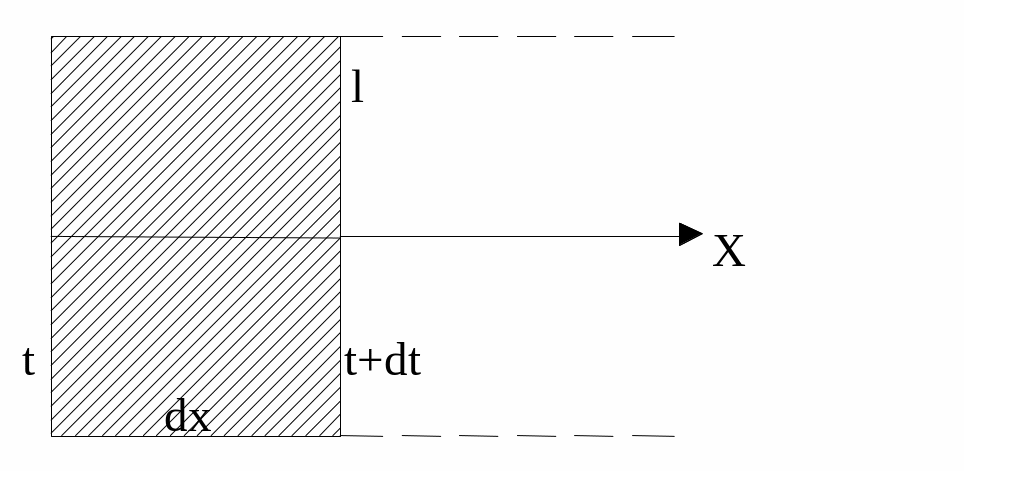
Під час руху замкненого провідника в зовнішньому магнітному полі, в його контурі виникає ЕРС індукції, що дорівнює швидкості зміни потоку індукції крізь поверхню, обмежену контуром.

Якщо в контурі рухається декілька ділянок, то ЕРС дорівнює алгебраїчній сумі швидкостей.

(9.15)

2. Вихрове електричне поле.

Контур знаходиться в електричному полі, що змінюється з часом.

. З досліду . Нехай

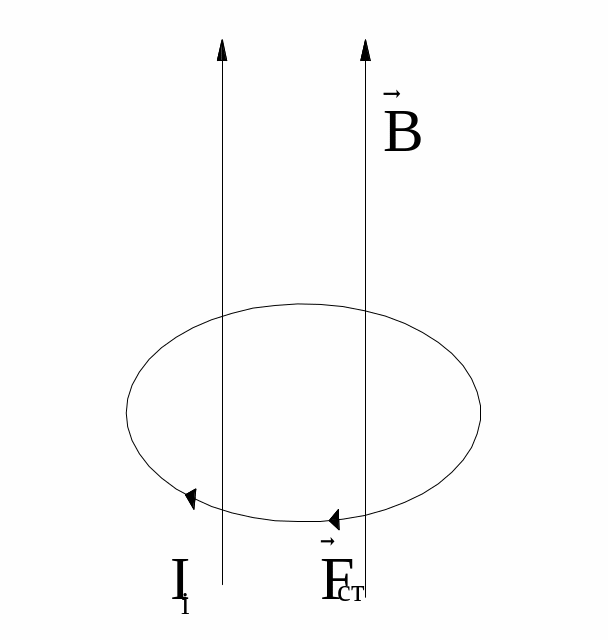
Ці сторонні сили не пов’язані ні з хімічними, ні з тепловими процесами в дроті, вони не можуть мати магнітну природу. Єдина можливість: повинні мати електричну природу – це означає, що в кожній точці провідника існує електричне поле.

Гіпотеза Максвела:

Будь-яке змінне в часі магнітне поле збуджує в оточуючому просторі електричне поле.

Згідно з визначенням ЕРС маємо:

(9.16)

(9.17)

(9.16) і (9.17) рівняння являють собою закон електромагнітної індукції в трактовці Максвела.

(9.17): Швидкість зміни магнітного поля визначає ротор напруженості поля в цій самій точці.

У відповідності з тим, що і , електричне поле не потенціальне.

Електричне поле, що збуджується змінним магнітним полем – вихрове.

Якщо , то

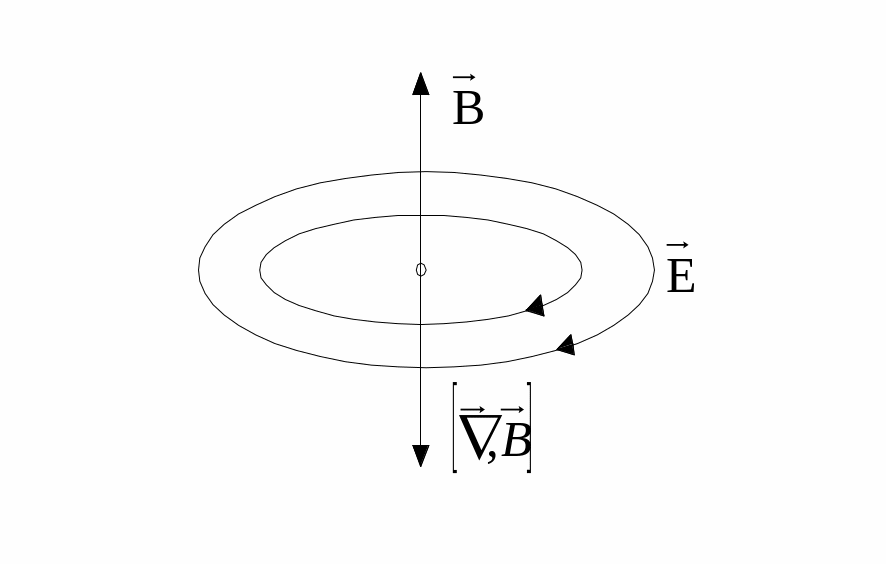
Лінії замкнені тому, що .

Формулювання Максвела більш загальне, ніж формулювання Фарадея. Максвел бачить сутність електромагнітної індукції в збудженні електричного поля.

3 . Відносність механізмів електромагнітної індукції

У загальному випадку, коли провідник рухається в змінному магнітному полі, індукційний струм виникає внаслідок дії повної сили Лоренца .

Оскільки існує взаємозвязок між електричним і магнітним полем, то розглядати їх окремо некоректно.

Розділ 10. Рівняння Максвела.

§1 Струм зміщення.

(10.1)

(10.2)

В стаціонарному випадку , ,

. Отже,рівняння (1) і (2) взаємоузгодженні.

, ,  (1) і (2) взаємосуперечливі.

За Максвелом: ,

, ,

(10.3)

Струм зміщення являє собою електричне поле, що змінюється в часі. З усіх фізичних властивостей, що має дійсний струм, струм зміщення має лише одну здатність  утворювати магнітне поле.

(10.4)

(10.5)

(10.6)