§1 Потік магнітного поля. Теорема Гауса для магнітного поля в вакуумі.

Нехай в просторі задана деяка поверхня S будь-якої форми. Виділимо елементарну площадку dS.

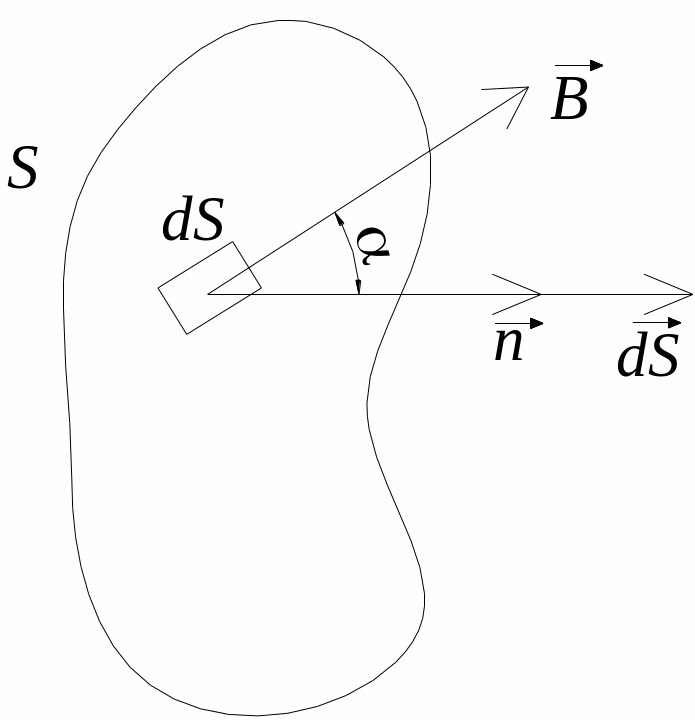
(7.1)

[Ф]=1Вб=1Тлм²=1Нм²/Ам=1Вс

1Вб – це потік магнітного поля при індукції 1Тл крізь площадку в 1м², розташовану  до вектора .

- кількість магнітних ліній, що виходять і входять в замкнену поверхню.

- поле заряда q, який рухається рівномірно і повільно.

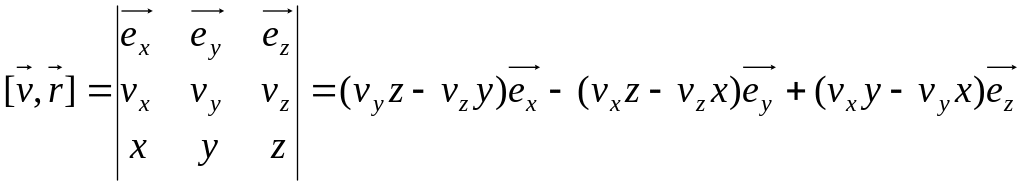
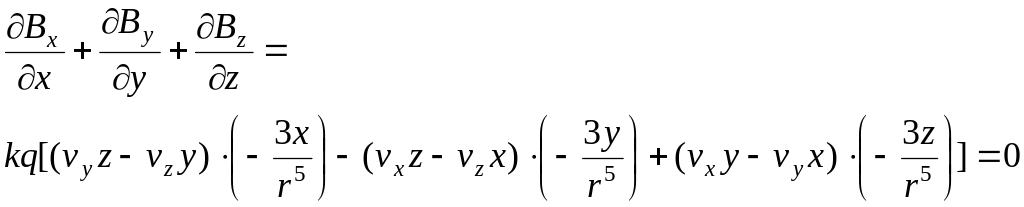
(7.2)

Вираз (7.2) є теорема Гауса в локальній (або диференціальній) формі:

дивергенція магнітного поля всюди дорівнює нулю.

Дивергенція  це питома алгебраїчна потужність джерел. Отже, в природі не існує магнітних зарядів, які були б джерелами магнітного поля.

За теоремою Остроградського-Гауса:

, S це замкнена поверхня, яка оточує обєм V. Отже, (7.3)

Це теорема Гауса для магнітного поля в вакуумі в інтегральній формі:

потік вектора магнітної індукції крізь довільну замкнену поверхню дорівнює нулю.

Отже, лінії магнітного поля завжди замкнені.

§2 Теорема про циркуляцію магнітного поля у вакуумі.

Ц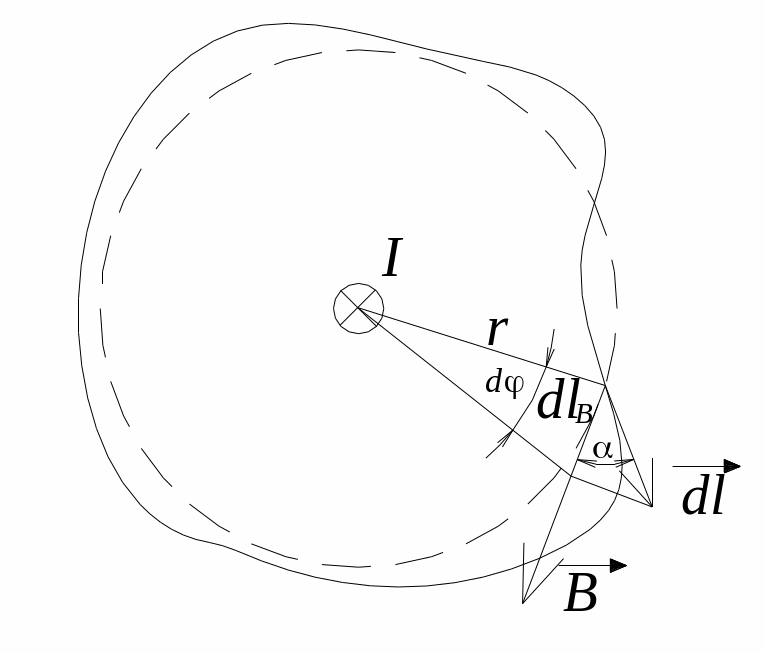 иркуляція вектора :

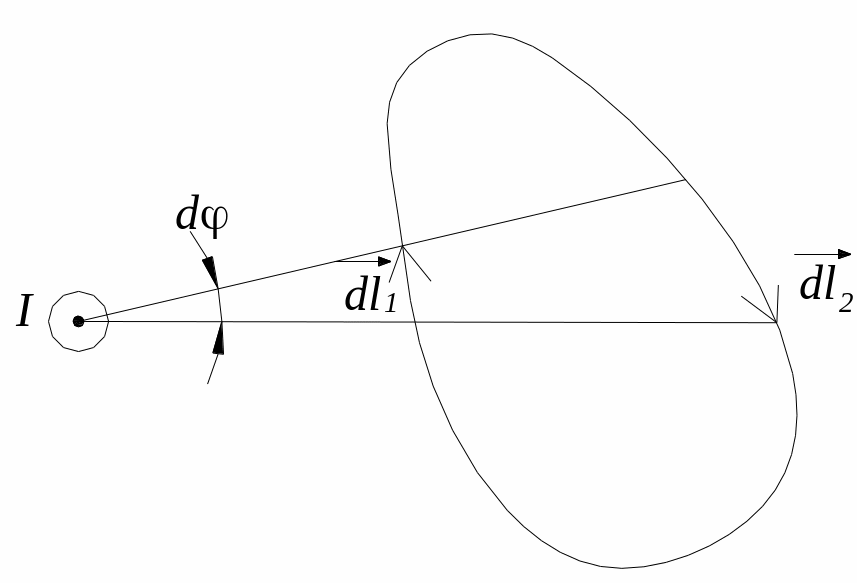
Розглянемо прямий струм у тонкому провіднику, обмежимо його плоским контуром довільної форми.

Отже, циркуляція вектора за контуром l дорівнює добутку магнітної сталої на силу струму, що охоплюється цим контуром.

Якщо струм не охоплюється контуром:

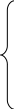
, якщо струм

охоплюється

контуром

0, якщо струм

не охоплюється

контуром

інтегрування

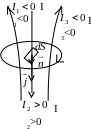
Знак циркуляції може бути “+” і “”. Знак циркуляції можна врахувати, вважаючи I алгебраїчною величиною. Додатнім вважають струм, напрямок якого повязують з напрямом правила правого свердлика.

Н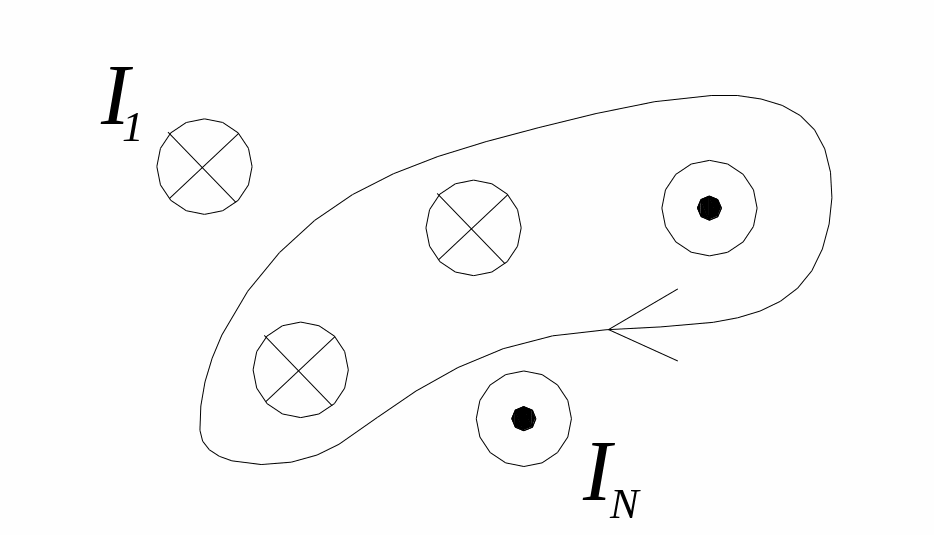 ехай маємо струми I₁, I₂,…, I_N .

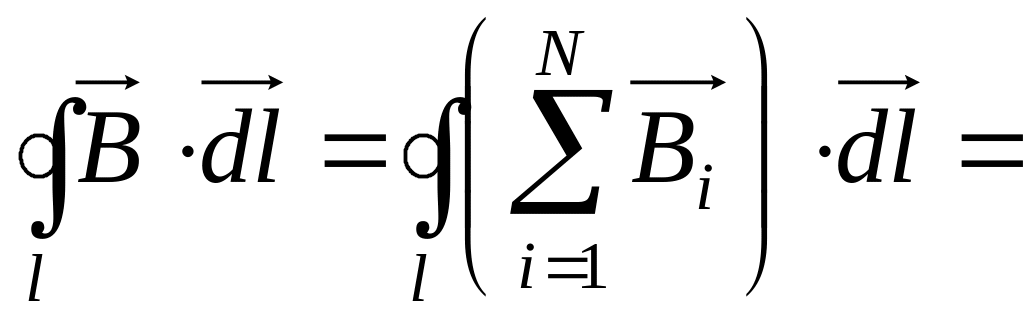
(7.4)

Циркуляція магнітного поля (вектора ) постійних струмів в вакуумі за довільним контуром l дорівнює добутку магнітної сталої на алгебраїчну суму струмів, що охоплюються цим контуром.

(7.5)

Той факт, що циркуляція вектора в загальному випадку не дорівнює нулю, говорить про те, що магнітне поле не є потенціальним на відміну від електростатичного.

Поняття скалярного потенціалу відсутнє.

§3 Обчислення магнітних полів за допомогою теореми про циркуляцію.

1) Магнітне поле прямолінійного провідника радіуса R нескінченної довжини з струмом I.

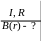
1.

2.

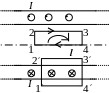
2) Магнітне поле нескінченно довгого соленоїда

n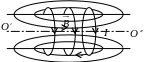 – кількість витків на одиницю довжини

Можна показати, що магнітне поле нескінченно довгого соленоїда зосереджене всередині каркаса, а назовні відсутнє взагалі.

У будь-якій точці соленоїда поле однорідне, і в будь-якій точці магнітна індукція дорівнює значенню магнітної індукції на осі.

(7.6)

nI – кількість ампер-витків.

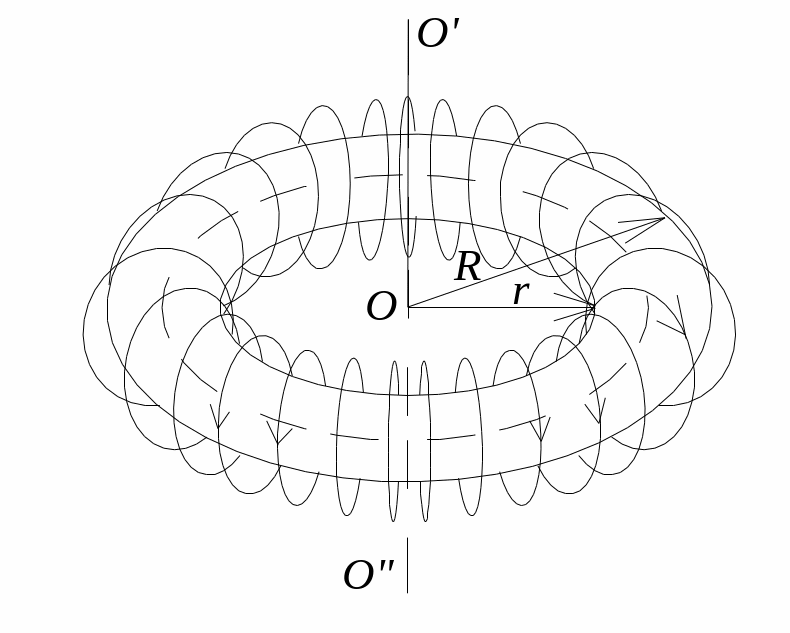
3) Магнітне поле тороїда

(7.7)

Алгоритм розвязку задач:

Аналіз симетрії магнітного поля.

Раціональний вибір контура.

Безпосереднє обчислення циркуляції вздовж контура.

Застосування теореми і вираження .