5)Количество информации. Измерение информации. Единицы измерения.

Математическое понятие информации тесно связано с ее измерением. Существуют два подхода (способа) измерения количества информации.

1. Энтропийный

2. Объемный

Энтропийный способ применяется в теории информации. Он учитывает ценность или полезность информации для человека. Способ измерения основан на следующей модели: пусть получателю сообщения известны определенные представления о возможном наступлении некоторых событий. Число событий обозначим n. В общем случае эти представления недостоверны и характеризуются вероятностью их наступления P_i. i=1,n. Общая мера неопределенности (энтропия) — H — математическая величина, зависящая от совокупности вероятностей — вычисляется по формуле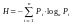 . В теории информации a=2, единица измерения называется бит.

Количество полезной информации в сообщении определяется тем, насколько уменьшается энтропия после получения сообщения. Существуют два крайних случая: сообщение называют тривиальным если оно не несет полезной информации (H_н=H_к); сообщение называется полным, если оно полностью снимает всю неопределенность (H_к=0).

В технике используют объемный способ измерения количества информации. Он основан на подсчете числа символов в сообщении, то есть связан с его длиной и не учитывает полезность информации для человека. Длина сообщения зависит от мощности используемого алфавита. То есть числа различных символов для записи сообщения. В СВТ используется двоичный алфавит, то есть сообщения записываются с помощью двух символов — 0 и 1. Один разряд двоичной записи называется бит. Также используется единица измерения байт — один символ сообщения, представленный восьмиразрядным двоичным кодом. На практике используются более крупные единицы измерения(килобайт, мегабайт, гигабайт, терабайт, петабайт...).

Эти два способа измерения — энтропийный и объемный, как правило, не совпадают, причем энтропийное количество информации не может быть больше числа символов в сообщении. Если же оно меньше, то говорят, что сообщение избыточно. На основе понятий энтропии и количества информации вводятся важные характеристики информационных систем:

1.Скорость создания информации — энтропия источника, отнесенная к единице времени, бит/с.

2.Скорость передачи информации — количество информации, переданное по каналу связи за единицу времени, бит/с.

3.Избыточность сообщений и сигналов — безразмерная величина, показывающая, какую долю полезной информации несет сообщение или сигнал.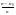 Где n₀- минимальная из длин сообщений, несущих аналогичную полезную информацию. Избыточность вредна, но она является информационным средством.

6)Кодирование информации. Двоичная система счисления. Кодировочные таблицы. Растровая и векторная графика.

Кодирование — это представление информации в виде определенных символических структур. Чаще всего используют одномерные представления, когда сообщение записывается в виде цепочки символов(например в письменных текстах, при передаче по каналу связи, при обработке в СВТ). Также используют многомерные представления. Например — всевозможные схемы, рисунки, макеты, схемы. В узком смысле под кодированием понимают переход от исходного представления для последующей передачи, обработки, хранения. В этом смысле обратный переход к исходному представлению называют декодирование. При кодировании ставятся различные цели и применяются различные методы. Наиболее распространенными целями являются:

1.Экономность сообщения, то есть снижение избыточности.

2.Повышение скорости передачи и обработки.

3.Надежность — защита информации от несанкционированного доступа.

4.Сохранность — защита информации от случайных искажений.

5.Удобство физической реализации (именно с этой целью в СВТ используют двоичное кодирование).

6.Удобство восприятия информации.

Указанные цели часто противоречат друг другу, так обеспечение надежности требует введения в сообщении дополнительных символов, то есть делает их неэкономными. То же самое происходит при обеспечении сохранности. Например, в финансовых документах числа часто записывают не в виде цифр, а словами, поскольку искажение или потеря цифры изменяет число, а искажение одной буквы — нет. В ходе сложного информационного процесса могут изменяться цели кодирования, и информация неоднократно перекодируется, например, в процессе создания компьютерной программы сначала алгоритм записывается словесно, затем представляется в виде графической схемы, далее переводится на язык программирования, и, в конечном итоге,

представляется в виде двоичных машинных кодов. Одним из основных принципов построения и функционирования СВТ является принцип двоичного кодирования, то есть все виды данных (числовые, графические, текстовые, аудио- и видеоданные) представляются в двоичном коде, то есть в виде последовательности двоичных разрядов.

Представление числовых данных.

В двоичной системе числовые данные представляются аналогично тому, как они строятся в десятичной системе. Каждому двоичному разряду ставится в соответствие его вес, равный соответствующей степени двойки (самый младший 2⁰=1, затем 2¹=2, 4, 8, и т.д.).

Представление символьных данных.

Для того, чтобы записать текст в двоичном коде, нужно каждый символ заменить некоторым числом, например порядковым номером символа в определенной таблице. Такая таблица устанавливает соответствие между символом и его кодом. Одного байта достаточно, чтобы закодировать 2⁸=256 различных символов. Такие таблицы называются восьмиразрядными. Этого достаточно, чтобы закодировать буквы естественного языка (английского и русского), математические символы, цифры, знаки препинания. Весь мир должен воспринимать текстовые данные одинаково — нужны единые, стандартизованные кодировочные таблицы. К сожалению, на сегодняшний день существует большое число различных кодировочных таблиц, учитывающих как национальные алфавиты, так и интересы фирм-производителей ПО. Была сделана попытка создания универсальной 16-разрядной таблицы Unicode.

Представление графических данных.

При кодировании изображений используют 2 подхода:

1.Точечная (растровая) графика

2.Векторная графика

В точечной графике изображение строится из большого числа отдельных точек (пикселей). Для каждого пикселя в числовой форме (в виде кода) задаются координаты на экране или бумаге, а также свойства, такие как яркость и цвет. Недостаток такого кодирования — большой объем данных (используется компрессия изображений). Плюс — можно кодировать любые произвольные изображения.

В векторной графике изображение строится из стандартных геометрических фигур (линия, прямоугольник, окружность..). Для каждой фигуры в числовой форме задаются ее тип, координаты, свойства. Такой подход дает более компактный объем данных для кодирования. Недостаток — область применения ограничена геометрически-правильными изображениями.

Представление аудио- и видеоданных.

Аудио- и видеоданные — потоковые данные, изменяющиеся во времени. В исходном виде — аналоговые сигналы. Для перевода их в числовую форму используют аналого-цифровые преобразователи (АЦП). Сам процесс называется квантованием или оцифровкой. Качество звука или видео будет определяться разрядностью преобразования (какое количество двоичных разрядов обрабатывается одновременно).