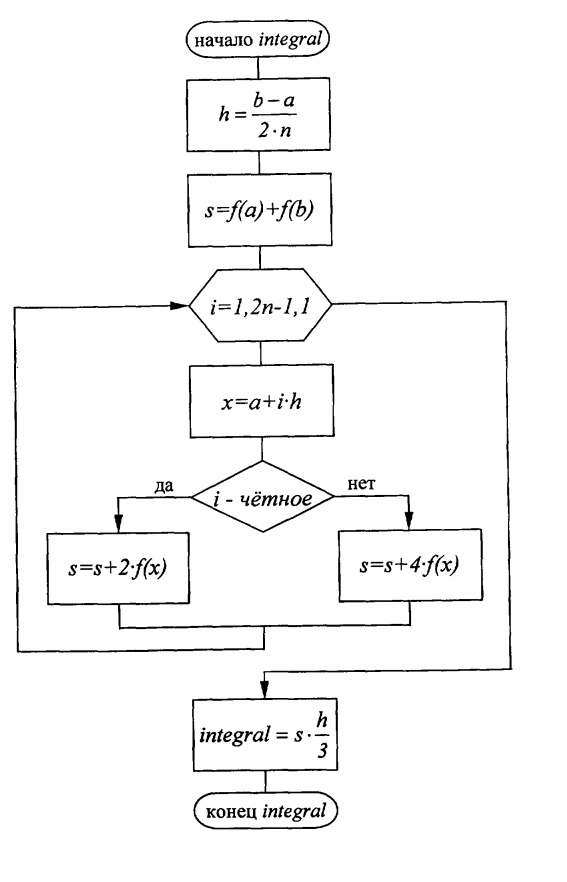
55. Численное интегрирование по методу Симпсона. Схема алгоритма

Метод Симпсона представляет интегрирование как сумму площадей параболических трапеций (сверху ограничены параболами). Поскольку для построения квадратичной параболы требуются 3 точки, то трапеции на 2 смежных отрезках разбиения.

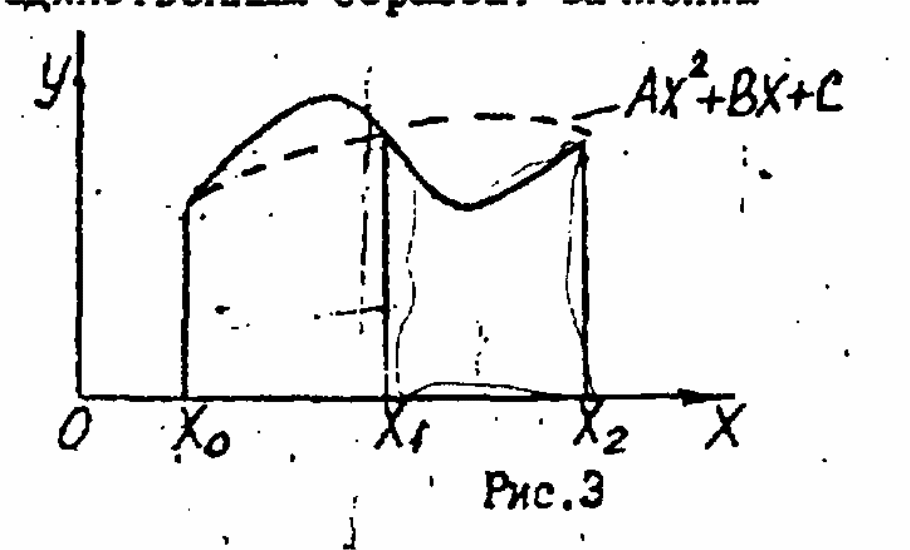
h=(b-a)/2n

2n – число отрезков разбиения

X_i=a+ih, i=0,1…2n

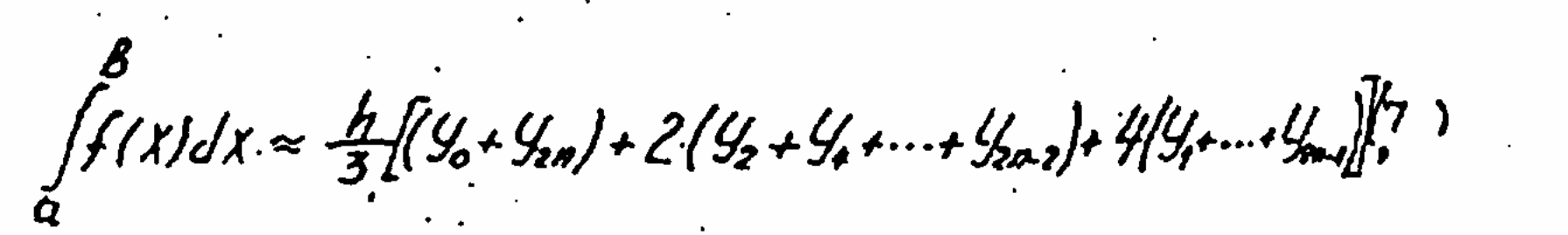
• Формула симпсона

Если подынтегральная функция функция y=f(x) имеет на отрезке [a,b] непрерывную четвертую производную, то для погрешности используется формула

Ɛ≤((b-a)⁵/(180n⁴))*M₄ , где M₄ – максимум модуля четвертой производной подынтегральной функции на заданном отрезке

Метод симпсона наиболее точный для вычисления приближенного значения интегралов.

56)Численное интегрирование двойных интегралов. Метод ячеек.

Для двойного интеграла область геометрически представляет собой плоскую произвольную фигуру, а значение интеграла – объем 3х мерной фигуры.

Метод ячеек.

Д анный метод применяется для вычисление 2х интегралов, когда область интегрирования D представляется собой прямоугольник.

I= f(x,y)dxdy ; D: a=<x=<b;c=<y=<d

Геометрически задача сводится к вычислению объема криволинейного параллелепипеда.

Идея вычисления: в геометрии нет готовой формулы для вычисления объема криволинейного параллелепипеда, то эту фигуру нужно приближенно заменить на прямоугольный, объем которого легко вычисляется.

Для снижения погрешности криволин.паралел-пипед разбиваем на множество более мелких.Вычисляем элементарные объемы и складываем.

Область интегр-я D разбивается на ячейки, соответственно исходный объем также разбивается n на m элементарных объемов.

h_y=(d-c)/m ; h_x=(b-a)/n; S=h_x*h_y – площадь ячейки; x_i=a+i*h_x; y_{i =}c+j*h_y

Для вычисления элементарного объема, S_ячейки умножают на значение подинтегральной ф-ции в центре ячеек x_i=(x_i+x_i-1)/2; y_i=(y_i+y_i-1)/2

с уммируя элементарные объемы получают приближенное значеиние 2ого интегрла. Формула ячеек -

f(x,y)dxdy = V=h_xh_y∑ⁿ∑^mf(xi,yi);

57)Метод последовательного интегрирования.

П 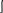усть для 2го интеграла область интегрирования D ограничена непрерывными кривыми:y=φ(x),y=ψ(x) и прямыми x=a,x=b;

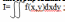= dx f(x,y)dy ; Пусть F(x)= f(x,y)dy; I= F(x)dx.

Внутренний и внешний интегралы явл. однократными и для их вычисления можно применить приближенные способы вычисления(прямоугольников, трапеций или метод Симсона).

П рименим формулу трапеций: I=h_x[F(a)+F(b)/2+∑^n-1F(x_i)] (1), где F(xi)-площади сечений исх.фигуры. эти площади вычислим используя формулу прямоуг.трапеций. для вычисления каждое сечение(в проекции хорду)разбиваем вдоль оси Оy с шаг h_y ; F(xi)= f(x,y)dy = h_y[f(x,y)+f(x,d)/2+∑_j ⁿ f(xi,yi)] (2)

Порядок расчета. Отрезок [a,b] разбивают с шагом h, в каждой точке x_i, вычисляют значения с=φ(x_i) ;d =ψ(x_i) – хорду [c,d] разбивают с шагом h_y.

Используя ф-лу (2) вычисл площади сечения F[xi,j=0,…n] по формуле (1) вычмсл значение 2го интеграла.

58) Обработка числовых данных.

Получение количественных результатов научных и технических задач приводят к необходимости обработки числовой информации. Данные часто предоставляются в табличной форме. Эти данные отражают функциональную зависимость одной величины от другой. В задаче аппроксимации требуется найти формулу выражающую функциональную зависимость аналитически. Сущ.2 основных подхода к решению данной задачи.1). состоит в построении интерполяционного многочлена,значения которого точно совпадают с табличными.Это достигается методами интерполяции(получ-я промежут значения). Геометрически требуется чтобы интерполирующая кривая y=P_n(x) проходила строго через все табличные точки. Однако совпадения значений в точках не означает совпадения характеров табличной и интерполирующей функций,так как данные экспериментальные – имеют свои погрешности измерения. Поэтому методы интерполяции принимают в узкой области вычисления промежуточных значений ф-ции.(метод интерполяции по Лагранжу,метод разделенных разностей) 2).Табличные данные аппроксимируют достаточно простой функцией применимой во всем диапазоне табличных данных, не обязательно проходящей через все точки. Такой подход называется подгонкой кривой ,кот-ю стремятся провести так, чтобы ее отклонения от табл точек были min.Обычно стремятся свести к мин сумму квадратов разностей м/у значениями,вычисленными по кривой и таблицей.+простота – большая погрешность.(Метод наименьших квадратов.)