
- •1) Предмет и задачи информатики.
- •2) Истоки и предпосылки информатики.
- •3) Структура современной информатики.
- •4) Понятие информации. Носители данных. Сигналы.
- •5)Количество информации. Измерение информации. Единицы измерения.
- •7)Свойства информации.
- •8) Устройство персонального компьютера. Основные узлы компьютера и их назначение.
- •9) Основные принципы построения и работы компьютера.
- •10)Хранение информации в компьютере. Понятие файла. Файловая система.
- •11)Понятие информационной технологии.
- •12)Понятие о компьютерных сетях. Локальные и глобальные сети.
- •13)Основы интернета.Основные протоколы
- •14)Службы интернета
- •15) Этапы подготовки задач для программирования и решения на компьютере.
- •16)Понятие алгоритма. Требования, предъявляемые к алгоритмам.
- •17)Методы проектирования алгоритмов.
- •18)Способы описания алгоритмов. Основы графического способа.
- •19)Типовые структуры алгоритмов. Основные виды вычислительных процессов. Примеры.
- •20)Вычисление суммы числового ряда
- •22)Сортировка элементов в массиве
- •3.6.1. Сортировка методом "пузырька"
- •3.6.2. Сортировка выбором
- •3.6.3. Сортировка вставкой
- •23Системы программирования и их состав.
- •24. Понятие о программировании. Языки программирования. Уровни языков
- •25.По, классификация
- •26. Ос, назначение, примеры
- •27)Основные функции ос
- •30)Основные элементы языка паскаль, описание констант и переменных, примеры
- •31)(Паскаль) Типы данных. Объявление типа данных в тексте программы. Преобразования типов.
- •32)Выражения паскаль. Основные операции, их приоритет.
- •33)Операторы паскаль, составной оператор, операторные скобки, опер-р присваивания значений, примеры
- •34)Ввод/вывод данных паскаль. Использ-е стандартных процедур ввода/вывода. Примеры использ-я Ввод данных
- •Вывод данных
- •35)Условный оператор паскаль, ветвление программы, примеры
- •37)Метки паскаль, оператор безусловного перехода, примеры
- •38)(Паскаль) Счетные операторы цикла. Примеры использования
- •39)(Паскаль) Оператор цикла с предпроверкой условия. Примеры использования
- •40)(Паскаль) Оператор цикла с постпроверкой условия. Примеры использования
- •41)Подпрограммы как основной элемент создания программ, метод нисходящего проектирования
- •42)Процедуры и функции. Правила записи в программе. Примеры.
- •43)Процедуры, правила обращения к процедурам, передача данных в процедуру и обратно. Отличие функции от процедуры, примеры.
- •44)Численное решение нелинейного уравнения. Этапы решения.
- •45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм.
- •47) Уточнение корня нелинейного уравнения методом касательных. Схема алгоритма.
- •49) Уточнение корня нелинейного уравнения методом простой итерации. Схема алгоритма.
- •50) Численное решение системы линейных уравнений методом исключения Гаусса. Схема алгоритма.
- •51) Численное решение системы нелинейных уравнений методом простых итераций. Схема алгоритма.
- •52.. Численное решение системы нелинейных уравнений методом Ньютона. Схема алгоритма.
- •53. Численное интегрирование по методу прямоугольников.
- •55. Численное интегрирование по методу Симпсона. Схема алгоритма
- •56)Численное интегрирование двойных интегралов. Метод ячеек.
- •57)Метод последовательного интегрирования.
- •59)Интерполяция по Лагранжу.
- •60. Метод разделенных разностей.
- •61) Аппроксимация табличных данных квадратичной функции по методу наименьших квадратов.
- •62) Аппроксимация табл данных обратно пропорц функции по мнк
- •63)Аппроксимация табличных данных показательной функции по методу наименьших квадратов. Схема.
- •64)Аппроксимация табличных данных степенной функции по мнк.
Метод
простой итерации по существу является
развитием этого же метода для одного
ур. Он основан на допущении, что систему
уравнений можно привести к виду:
Если
исходные значения слишком сильно
отличаются от истинного решения, то
процесс не сойдется. Область, в которой
заданные исходные значения сходятся
к решению, называется областью сходимости.
Если исх. значения лежат за пределами
этой области, то решение получить не
удастся.
Условия,
при которых метод итерации сходится к
решению, математически задаются системой
неравенств:
Алгоритм
метода:51) Численное решение системы нелинейных уравнений методом простых итераций. Схема алгоритма.
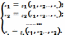 Задают
исх. приближения
,
подставляют их в ф.
Задают
исх. приближения
,
подставляют их в ф.  и
последовательно вычисляют новые
значения
и
последовательно вычисляют новые
значения  по
схеме:
по
схеме: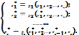 Зн.
сравнивают
с
и выясняют, достаточно ли мало различие
между ними. Если каждая переменная
изменилась на достаточно малую величину,
т.е.
Зн.
сравнивают
с
и выясняют, достаточно ли мало различие
между ними. Если каждая переменная
изменилась на достаточно малую величину,
т.е. 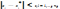 то
расчет прекращается. В противном случае
процесс повторяется, причем зн.
исп. в качестве новых исходных значений
неизвестных.
то
расчет прекращается. В противном случае
процесс повторяется, причем зн.
исп. в качестве новых исходных значений
неизвестных.
 С увеличением числа уравнений область
сх-ти уменьшается и в случае больших
систем сх-ть обеспечивается лишь при
условии, что исходные значения переменных
очень близки к истинному решению.
С увеличением числа уравнений область
сх-ти уменьшается и в случае больших
систем сх-ть обеспечивается лишь при
условии, что исходные значения переменных
очень близки к истинному решению.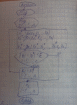
Метод
Ньютона отличается от м.простой итерации
лучшей сходимостью. Основан на разложении
нелинейных ф. в сходящийся ряд и исп.
линейной части разложения для получения
решения.
Предположим
для системы:
Подставим
точное решение в исх. систему уравнений:
Предполагая,
что ф.
Приведем
получившуюся линейную систему к трад.
виду:
Вычисл.
поправки позволяют перейти кслед. k+1
приближению решения:
Оно
не совпадает с точным решением, но
прибл. к нему. Если на очередной итерации
все поправки становятся дост. малыми
(<заданной погр. Е), то расчет прекращается.52.. Численное решение системы нелинейных уравнений методом Ньютона. Схема алгоритма.
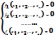 Пусть
известно k-ое
приближение к истинному решению (
Пусть
известно k-ое
приближение к истинному решению (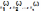 ).
Тогда точное решение
).
Тогда точное решение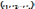 можно представить в виде (
можно представить в виде (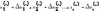 ),
где
),
где 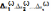 –поправки(погр.
истинного решения)
–поправки(погр.
истинного решения)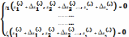 Неизвестными в этой системе являются
поправки
Неизвестными в этой системе являются
поправки
 непрерывно
дифф. В некоторой выпуклой области,
содержащей
непрерывно
дифф. В некоторой выпуклой области,
содержащей 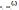 ,
разложим левые части уравнений в
степенные ряды, огр. Линейными членами:
,
разложим левые части уравнений в
степенные ряды, огр. Линейными членами: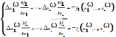 Такую
систему линейных уравнений можно решить
прямым методом(м. Гаусса) и получить
значения поправок
Такую
систему линейных уравнений можно решить
прямым методом(м. Гаусса) и получить
значения поправок
53. Численное интегрирование по методу прямоугольников.
По методу прямоугольников подынтегральная кривая представляется в виду кусочно-линейной функции, отрезки которой параллельны оси абсцисс.
Промежуток интегрирования [a,b] делится на n равных отрезков длиной h.
h=(b-a)/n
ui=a+i*h, i=0,1,...,n;
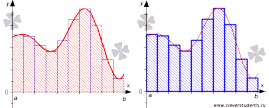
В зависимости от выбранного метода аппроксимации формулы прямоугольников могут быть представлены в различном виде.
а) Метод левых прямоугольников

Погрешность достаточно велика.
б) Метод правых прямоугольников
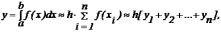
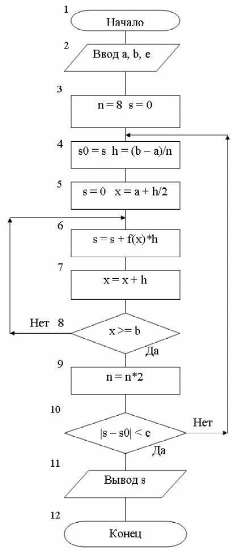
54)Численное интегрирование по методу прямоугольных трапеций. Схема алгоритма.
Метод трапеций использует линейную интерполяцию, т.е. график функции у=f(х) представляется в виде ломаной, соединяющей точки (хi, уi). В этом случае площадь всей криволинейной трапеции складывается из площадей элементарных прямоугольных трапеций (рис.7.4 а, 7.4 б)
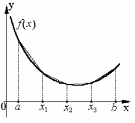 Рис.7.4 а
Рис.7.4 а
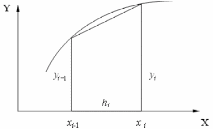 Рис.7.4 б
Рис.7.4 б
Площадь каждой такой трапеции определяется по формуле:
|
(7.8) |
 ,
где n -
число интервалов разбиения.
,
где n -
число интервалов разбиения.
Складывая все эти равенства, получим формулу трапеций для численного интегрирования:
|
(7.9) |
или
|
(7.10) |
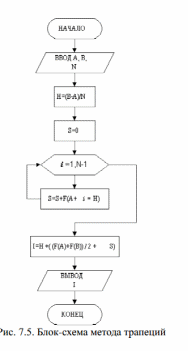
Формулы (7.9) и (7.10) можно представить в виде:
|
(7.11) |
|
(7.12) |

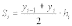 ,
i=1,2,...,n .
,
i=1,2,...,n .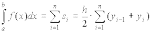 ,
, .
. ,
,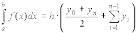 .
.