47) Уточнение корня нелинейного уравнения методом касательных. Схема алгоритма.
О
тличие
от м.хорд – вместо хорды на каждом шаге
проводится касательная к кривой y=f(x)
и в качестве приближения к корню ищется
точка пересечения касательной с осью
абсцисс. Уравн-е касательной проведенной
в т. х0
:
.
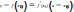Правило: В качестве исходной точки х0
выбирается тот конец интервала [a,b]
, где знак ф-и совпадает со знаком 2й
производной f’’(x).
Из уравнения касательной найдем
след.приближение корня х1
, как абсциссу точки пересечения
касательной с осью ох : 
.
Аналогично м. б. найдены и последующие
приближенно. Ф-ла для i+1
приближения имеет вид :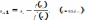
Для окончания можно использовать условия
|f(xi)|<e
или |xi+1-xi|<e.
Алгоритм:
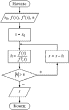
4
8)
Уточнение корня нелинейного уравнения
комбинированным методом. Схема
алгоритма.Геометрически
такое объединение сводится к тому, что
приближение к истинному значению корня
уравнения f(x)=0
на каждой итерации происходит одновременно
с 2х сторон интервала [a,b].
При это, для приближения к корню с одной
стороны строится хорда, а с др.- касательная.
Пусть для определенности f’(x)>0
и f’’(x)>0
при a≤x≤b.
Тогда для приближения к корню со стороны
границы а используем построение хорды,
а со стороны границы b
– касательная. На 1й итерации строим
хорду А0В0
и проводим касательную в точку В0.
Левую границу а переносим в а1,
правую – b1.
На каждой
итерации для вычисления новых границ
интервала используют ф-лы хорд и
касательных :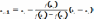 
,
.
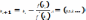Сужение интервала проводим до тех пор
пока он не станет < зад.погрешности
|bi+1-ai+1|<e.
За значение корня можно взять среднее
арифметическое полученных границ
интервала.
Алгоритм:
49) Уточнение корня нелинейного уравнения методом простой итерации. Схема алгоритма.
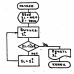
Исходное уравнение f(x)=0 заменяется равносильным уравнением x=g(x)(1). Это уравнение можно представить в виде системы :y=x; y=(x) (2). Пусть известно начальное приближение корня x=x0 . Подставляя это значение в правую часть уравнения (1) получим новое приближение x1= g(x0). Далее подставляя каждый раз новое приближение корня в правую часть (1), получаем последовательность значений xi+1=g(xi), (i=0,1,…). Итерационный процесс сходится к истинному значению корня, если с увеличением числа итераций значения хi+1 и xi сближаются. Процесс продолжают до тех пор пока не будет обнаружено, что |xi+1-xi|<e. Условие сходимости. Если |g’(x)|<1, то выполняется условие т.о., в методе итераций важно правильно выбрать вид ф-и g(x) и значение начального приближения х0. Уравнение f(x)=0 можно преобразовать след.образом x=x-m*f(x), m-отличная от нуля const. В этом случае g(x)=x-m*f(x). Ф-яg(x) должна удовлетворять условию сходимости |g’(x)|<1, т.о. |1-m*f’(x)|<1. Нужно подобрать m так, чтобы для всех х из [a,b] это условие соблюдалось. Алгоритм:
50) Численное решение системы линейных уравнений методом исключения Гаусса. Схема алгоритма.
Система
линейных уравнений в матричном виде:
Ax=b,
где A=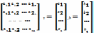
,
если А неособенная, т.е. detA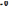
,
то система или эквивалентное ей матричное
уравнение имеет единств. Решение.
Исходную системус матрицей коэф. А приводят путем экв. преобразований к системе с треугольной матрицей:
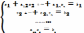Решение
системы треугольно вида можно легко
вычислить по рекурр. формулам: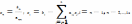 
(1) Вычислительная процедура:
1)
Прямой ход. Сначала нормируют Iур.,
для этого его коэф. делят на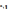 
,
затем Iур.
Умножают на первые коэф. 
всех
нижестоящих ур., кроме первого. Далее
такая же процедура применяется к
остальным n-1
ур. В результате Система будет приведена
к верхнему треуг. виду.
Математический алг.: на k-ом шаге процесса исключения новые нормированные коэф. k-го уравнения (его называют ведущим) имеют вид:
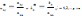Новые
коэф. в
уравнениях, стоящих ниже ведущего,
принимают вид:
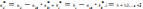
J=1,2,…,n.
2)
Обратный ход. Значения неизвестных
вычисляются
по формулам (1).
Применение м. Гаусса усложняется, если диаг. коэф. ведущего ур. равен 0. В этом случае ведущееур. Нельзя нормировать. Однако, изменив порядок уравнений, эту трудность можно обойти.
Наим.погрешность округления достигается, когда диаг. коэф. (ведущий эелемент) имеет наиб. значение. Поэтому строку с нулевым или малым вед.элементом заменяют на ту из стоящих под ней строк, в которой в том же столбце стоит эл-т с наиб. значением. Такая процедура наз. методом Гаусса с выбором ведущего эл-та.
