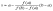- •1) Предмет и задачи информатики.
- •2) Истоки и предпосылки информатики.
- •3) Структура современной информатики.
- •4) Понятие информации. Носители данных. Сигналы.
- •5)Количество информации. Измерение информации. Единицы измерения.
- •7)Свойства информации.
- •8) Устройство персонального компьютера. Основные узлы компьютера и их назначение.
- •9) Основные принципы построения и работы компьютера.
- •10)Хранение информации в компьютере. Понятие файла. Файловая система.
- •11)Понятие информационной технологии.
- •12)Понятие о компьютерных сетях. Локальные и глобальные сети.
- •13)Основы интернета.Основные протоколы
- •14)Службы интернета
- •15) Этапы подготовки задач для программирования и решения на компьютере.
- •16)Понятие алгоритма. Требования, предъявляемые к алгоритмам.
- •17)Методы проектирования алгоритмов.
- •18)Способы описания алгоритмов. Основы графического способа.
- •19)Типовые структуры алгоритмов. Основные виды вычислительных процессов. Примеры.
- •20)Вычисление суммы числового ряда
- •22)Сортировка элементов в массиве
- •3.6.1. Сортировка методом "пузырька"
- •3.6.2. Сортировка выбором
- •3.6.3. Сортировка вставкой
- •23Системы программирования и их состав.
- •24. Понятие о программировании. Языки программирования. Уровни языков
- •25.По, классификация
- •26. Ос, назначение, примеры
- •27)Основные функции ос
- •30)Основные элементы языка паскаль, описание констант и переменных, примеры
- •31)(Паскаль) Типы данных. Объявление типа данных в тексте программы. Преобразования типов.
- •32)Выражения паскаль. Основные операции, их приоритет.
- •33)Операторы паскаль, составной оператор, операторные скобки, опер-р присваивания значений, примеры
- •34)Ввод/вывод данных паскаль. Использ-е стандартных процедур ввода/вывода. Примеры использ-я Ввод данных
- •Вывод данных
- •35)Условный оператор паскаль, ветвление программы, примеры
- •37)Метки паскаль, оператор безусловного перехода, примеры
- •38)(Паскаль) Счетные операторы цикла. Примеры использования
- •39)(Паскаль) Оператор цикла с предпроверкой условия. Примеры использования
- •40)(Паскаль) Оператор цикла с постпроверкой условия. Примеры использования
- •41)Подпрограммы как основной элемент создания программ, метод нисходящего проектирования
- •42)Процедуры и функции. Правила записи в программе. Примеры.
- •43)Процедуры, правила обращения к процедурам, передача данных в процедуру и обратно. Отличие функции от процедуры, примеры.
- •44)Численное решение нелинейного уравнения. Этапы решения.
- •45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм.
- •47) Уточнение корня нелинейного уравнения методом касательных. Схема алгоритма.
- •49) Уточнение корня нелинейного уравнения методом простой итерации. Схема алгоритма.
- •50) Численное решение системы линейных уравнений методом исключения Гаусса. Схема алгоритма.
- •51) Численное решение системы нелинейных уравнений методом простых итераций. Схема алгоритма.
- •52.. Численное решение системы нелинейных уравнений методом Ньютона. Схема алгоритма.
- •53. Численное интегрирование по методу прямоугольников.
- •55. Численное интегрирование по методу Симпсона. Схема алгоритма
- •56)Численное интегрирование двойных интегралов. Метод ячеек.
- •57)Метод последовательного интегрирования.
- •59)Интерполяция по Лагранжу.
- •60. Метод разделенных разностей.
- •61) Аппроксимация табличных данных квадратичной функции по методу наименьших квадратов.
- •62) Аппроксимация табл данных обратно пропорц функции по мнк
- •63)Аппроксимация табличных данных показательной функции по методу наименьших квадратов. Схема.
- •64)Аппроксимация табличных данных степенной функции по мнк.
44)Численное решение нелинейного уравнения. Этапы решения.
f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.
Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.
Задача нахождения корней состоит из 2 этапов:
1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:
[ a;b]
– интервал изоляции корня. Для каждого
корня уравнения определяется интервал
его изоляции [a;b].
На отрезке [a;b]
должен находиться 1 корень.
a;b]
– интервал изоляции корня. Для каждого
корня уравнения определяется интервал
его изоляции [a;b].
На отрезке [a;b]
должен находиться 1 корень.
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.
Классификация методов уточнения корней :
1) Метод половинного деления отрезка(дихотомии).
О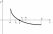 трезок
[a;b],
содержащий единственный корень, делят
пополам, отбрасывают ту половину, где
нет корня. Процесс повторяется до тех
пор, пока длина отрезка не станет меньше
заданной погр. E.
трезок
[a;b],
содержащий единственный корень, делят
пополам, отбрасывают ту половину, где
нет корня. Процесс повторяется до тех
пор, пока длина отрезка не станет меньше
заданной погр. E.
Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.
2) Метод хорд.
П остроение
последовательных хорд, в качестве
приближений к корню принимаются значения
их пересечения с осью абсцисс.
остроение
последовательных хорд, в качестве
приближений к корню принимаются значения
их пересечения с осью абсцисс.
Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).
3 )
Метод касательных( метод Ньютона)
)
Метод касательных( метод Ньютона)
В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.
Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).
4) Комбинированный метод – объединение методов хорд и касательных.
П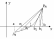 риближение
к корню на каждой итерации происходит
одновременно с 2 сторон интервала [a;b].
Одной стороны строится хорда, а с другой
касательная.
риближение
к корню на каждой итерации происходит
одновременно с 2 сторон интервала [a;b].
Одной стороны строится хорда, а с другой
касательная.
Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).
5) Метод простой итерации.
Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.
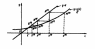
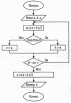
Требуется вычислить
корень уравнения f(x)=0
на [a;b]
с заданной погрешностью Е.
Отрезок [a;b],
содержащий единственный корень, делят
на 2 половины, отбрасывают ту из них,
где нет корня. Процесс продолжается до
тех пор, пока длина отрезка не станет
меньше заданной погрешности Е.
Алгоритм
метода:45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм.
4
6)Уточнение
корня нелинейного уравнения методом
хорд. Схема алгоритма.Требуется
вычислить корень уравнения f(x)=0
на [a,b]
с заданной погрешностью е. Геометр-ки
метод основан на построении
последовательности хорд. Ур-е хорды
 .
В данном методе процесс итерации состоит
в том, что в качестве приближений к корню
уравнение f(x)=0
принимаются значения х1,
х2…
хi
точек пересечения хорды АВ с осью
абсцисс. Если f(a)>0
, то левая граница a
неподвижна, х0=b
и из урав. хорды получим:
.
В данном методе процесс итерации состоит
в том, что в качестве приближений к корню
уравнение f(x)=0
принимаются значения х1,
х2…
хi
точек пересечения хорды АВ с осью
абсцисс. Если f(a)>0
, то левая граница a
неподвижна, х0=b
и из урав. хорды получим:  Если f(a)<0,
то правая граница b
неподвижна, x0=a.
Если f(a)<0,
то правая граница b
неподвижна, x0=a.
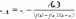 .
.
Алгоритм:
г де
Det_x
де
Det_x