20)Вычисление суммы числового ряда
Числовой ряд – это последовательность чисел, подчиняющаяся определенному закону.
Например:
Ряд натуральных чисел: 1, 2, 3, 4, 5, 6, …
Закон: каждый следующий элемент ряда на 1 больше предыдущего.
Задача: вычислить сумму чисел от 1 до 100.
Решение: обозначим сумму чисел - S.
Идея решения: каждое число от 1 до 100 нужно прибавлять к сумме.
Программа:
Program z1;
Var s, a: integer;
Begin
S:=0;
For a:=1 to 100 do
Begin
S:=S + a;
End;
Writeln(‘s=‘,s);
End.
Вычисление очередного слагаемого по рекуррентной формуле
Пусть необходимо вычислить сумму следующего вида:
.
На первый взгляд, для вычисления рассматриваемой суммы необходимо организовать вложенные циклы. При этом внешний цикл должен накапливать сумму y, а внутренний цикл должен вычислять факториал i!. Такой подход имеет ряд недостатков. К числу их следует отнести быстрое возрастание факториала i!. Это может привести к переполнению разрядной сетки. В то же время значение очередного слагаемого, определяемого величиной
может помещаться в разрядной сетке компьютера. Другой недостаток – необходимость в организации вложенных циклов.
Другой подход связан с использованием функциональной связи между двумя последовательными значениями слагаемых искомой суммы y. Обозначим эти значения слагаемых через Ai и Ai+1. Составим отношение этих слагаемых
При таком подходе отпадает необходимость в вычислении факториала i!. Кроме того, вычисления могут быть выполнены с помощью одного цикла (нет необходимости в организации вложенных циклов).
Следующий фрагмент программы реализует необходимые вычисления:
Y := 0;
A := sqr(sqr(x)) / 24;
For I := 4 To n Do
Begin
Y := Y + A;
A := A * X /(i + 1);
End;
21) Алгоритм поиска максимального (минимального) элемента одномерного массива. Пример.
Дан массив X, состоящий из n элементов. Найти максимальный элемент массива и номер, под которым он хранится в массиве.
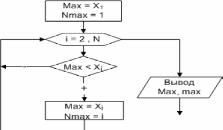
Алгоритм решения задачи следующий. Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax - его номер. Предположим, что первый элемент массива является максимальным, и запишем его в переменную Max, а в Nmax занесем его номер, то есть - 1. Затем все элементы, начиная со второго, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax - текущее значение индекса i. Процесс определения максимального элемента в массиве приведен в таблице 3.1 и изображен при помощи блок-схемы на рис. 3.7.
Таблица 3.1. Определение максимального элемента и его номера в массиве |
|||||||
Номера элементов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Исходный массив |
4 |
7 |
3 |
8 |
9 |
2 |
5 |
Значение переменной Max |
4 |
7 |
7 |
8 |
9 |
9 |
9 |
Значение переменной Nmax |
1 |
2 |
2 |
4 |
5 |
5 |
5 |
|
Рис. 3.7. Поиск максимального элемента и его номера в массиве |
Совет. Алгоритм поиска минимального элемента в массиве будет отличаться от приведенного выше лишь тем, что в условном блоке знак поменяется с > на <.