4. Детерминант. Его свойства.

Детерминант - одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы. В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы   детерминант определяется как

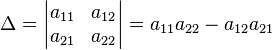
Для матрицы   определитель задаётся рекурсивно:

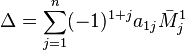,    где   — дополнительный минор к элементу  . Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы   такова:

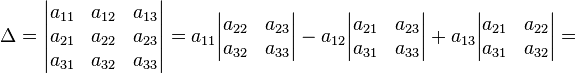
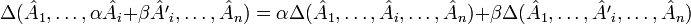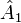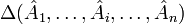• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):   , где  и т. д. — строчки матрицы,   — определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. Также формулу Бине-Коши).

• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

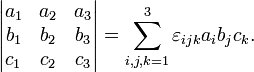
5. Метод Крамера.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).

Описание метода

Для системы   линейных уравнений с   неизвестными (над произвольным полем)

с определителем матрицы системы  , отличным от нуля, решение записывается в виде

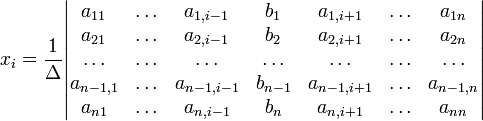
(1-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что   отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы   и  , либо набор   состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Система линейных уравнений:

Определители:

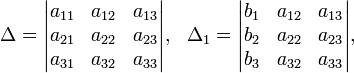
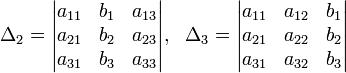
Решение:

Пример:

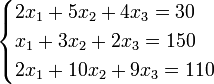
Определители:

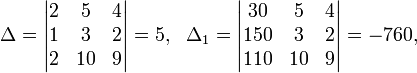
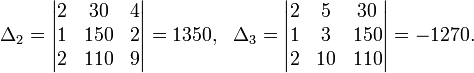
6. Обратная матрица. Ее свойства.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Свойства обратной матрицы

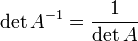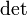• , где   обозначает определитель.

•  для любых двух обратимых матриц   и  .

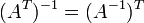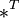•  где   обозначает транспонированную матрицу.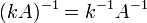

•  для любого коэффициента   .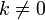

• Если необходимо решить систему линейных уравнений 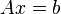 , (b — ненулевой вектор) где   — искомый вектор, и если 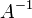  существует, то 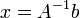 . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться следующим способом:

С помощью матрицы алгебраических дополнений

 — транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной натранспонированную матрицу алгебраических дополнений элементов исходной матрицы.

Пример

Матрица 2х2

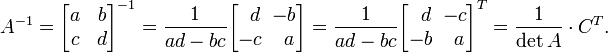
Обращение матрицы 2х2 возможно только при условии, что  .