Комплексные числа. Алгебраическая, тригонометрическая, геометрическая формы представления. Сопряжение. Формула Муавра.
Комплексные
числа - расширение поля вещественных
чисел.
Любое
комплексное число может быть представлено
как формальная сумма 
,
где 
и 
—
вещественные числа, 
—мнимая
единица.
Алгебраическая форма
Запись
комплексного числа 
в
виде
, 
,
называется алгебраической
формой комплексного
числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что 
):
Тригонометрическая и показательная формы
Если
вещественную
и
мнимую
части
комплексного числа выразить через
модуль 
и
аргумент 
(
, 
),
то всякое комплексное число
,
кроме нуля, можно записать в тригонометрической
форме
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
где 
—
расширение экспоненты для
случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
Геометрическая модель
Рассмотрим
плоскость с прямоугольной
системой координат.
Каждому комплексному числу 
сопоставим
точку плоскости с координатами 
(а
также радиус-вектор,
соединяющий начало координат с этой
точкой). Такая плоскость называется комплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются
соответственно вещественной и
мнимой осями.
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент).
В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое доказательство.
Сопряжённые числа
Если
комплексное число 
,
то число 
называется
сопряжённым (или
комплексно сопряжённым) к
(обозначается
также 
).
На комплексной плоскости сопряжённые
числа получаются зеркальным отражением
друг друга относительно вещественной
оси. Модуль сопряжённого числа такой
же, как у исходного, а их аргументы
отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
(сопряжённое
к сопряжённому есть исходное).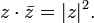
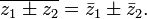
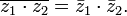
Формула
Муавра
для комплексных чисел 
утверждает,
что
для любого 