1) Физика — фундаментальная отрасль естествознания

Слово "физика" появилось еще в древние времена. В переводе с греческого оно означает "природа". Одно из основных сочинений древнегреческого философа и ученого Аристотеля (384- 322 до н. э.), ученика Платона, так и называлось "Физика". Физика тех времен, конечно, носила натурфилософский характер.

К настоящему времени известны четыре вида основных фундаментальных взаимодействий:

• гравитационное,

• электромагнитное,

• сильное,

• слабое.

• Гравитационное взаимодействие с телами и с массой

• Электромагнитное взаимодействие возникает в частицах, энергических зарядах.

• Сильное взаимодействие внутри ядерных ядер.

• слабое взаимодействие распад элементарных частиц проще фатонов.

2) Предмет и задачи физики

Фи́зика — область естествознания, наука, изучающая наиболее общие и фундаментальные закономерности, определяющие структуру и эволюцию материального мира. Более просто, физика — это наука о природе в самом общем смысле. Законы физики лежат в основе всего естествознания. Физика изучает вещество (материю) и энергию, а также фундаментальные взаимодействия природы, управляющие движением материи. Физические законы являются общими для всех материальных систем, поэтому физику можно называют «фундаментальной наукой».

В задачи физики входит  обнаружение ранее неизвестных явлений, подтверждение или опровержение физических теорий, формулирование общих законов природы (физических теорий) и объяснение на основе этих законов различных явлений, а также предсказание до сих пор неизвестных явлений, формулирование общих законов природы (физических теорий) и объяснение на основе этих законов различных явлений, а также предсказание до сих пор неизвестных явлений.

3) Связь физики с математикой

1. физика ставит задачи, решение которых приводит к появлению новых математических идей и методов, а они, в свою очередь, становятся базой для развития математической теории;

2. математическая теория с ее идеями и аппаратом применяется для изучения и анализа физических явлений, что приводит к созданию новой физической теории;

3. математический аппарат, на который опирается физическая теория, развивается по мере его использования в физике; происходит параллельный прогресс и физики, и математики.

4) Экспериментальная и теоретическая физика

Теорети́ческая фи́зика — раздел физики, в котором в качестве основного способа познания природы используется создание математических моделей явлений и сопоставление их с реальностью. В такой формулировке теоретическая физика является самостоятельным методом изучения природы

Эксперимента́льная фи́зика — способ познания природы, заключающийся в изучении природных явлений в специально приготовленных условиях. В отличие от теоретической физики, которая исследует математические модели природы, экспериментальная физика призвана исследовать саму природу.

5) Физические величины, их измерение и оценка погрешностей

Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точностиизмерения.

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

7) Краткая история физических идей, концепций и открытий

 Дерево в саду родового имения семьи Ньютонов в Вулсторпе,неподалёку от Кембриджа,откуда сорвалось знаменитое яблоко,в течение многих лет,пока его не сломала буря,было музейным экспонатом.Ещё бы!Падение этого яблока явилось причиной открытия закона всемирного тяготения!

   Простудившаяся жена профессора анатомии Болонского университета Луиджи Гальвани требовала заботы и внимания.Врачи прописали ей "укрепительный бульон'' из лягушечьих лапок.Приготовляя лягушек для бульона,Гальвани и открыл знаменитое '' животное электричество''-электрический ток.

    Адъюнкт кафедры фармацевтики Копенгагенского университета,профессор физики Ганс Христиан Эрстед в 1820 г. во время одной из своих лекций получил записку от студента,в которой тот обращал его внимание на поворот магнитной стрелки,находящейся на демонстрационном столе под проволокой,по которой проходил электрический ток.Так было положено начало изучению электромагнитных явлений.

    8 ноября 1895 г. профессору Вюрцбургского университета Вильгельму Конраду Рентгену не спалось.Он спустился в свою лабораторию и... открыл рентгеновские лучи.

     Итальянский физик Паули получил Нобелевскую премию благодаря посещению... театра. Он сформулировал знаменитый "принцип Паули" во время ревю в Копенгагенском театре.

8) Физика и научно-технический прогресс

Научно-технический прогресс – это непрерывный и сложный процесс открытия и использования новых знаний и достижений в хозяйственной жизни. В результате НТП происходит развитие и совершенствование всех элементов производительных сил: средств и предметов труда, рабочей силы, технологии, организации и управления производством.

         Физика одна из наук, являющейся основой научно-технического прогресса и активно участвующей в техническом развитии цивилизации.

         В начале 20 века величайшая революция в физике связана с возникновением квантовой теории относительности, физике атома.

         Примером технической революции может служить создание паровых и электрических двигателей, коренным образом изменивших лицо всей энергетики, создан принципиально новый вид передачи информации – космические средства связи, через специальные спутники связи, ретрансляционные центры.

         

         Мы видим, что все революционные преобразования в астрономии возникли на базе физических исследований (подводит краткий итог сообщения)

         Как видите, достижения физики позволили заглянуть в глубь живой материи.

         Как видим, чем больше физика развивается, как наука, тем глубже проникает она в тайны человеческого организма, тем теснее её взаимодействие с другими науками, и мы снова убеждаемся, что физика – основа и опора всех без исключения наук. Сделано много, но ёще предстоит сделать больше. Задачи надо решать сложные. И вам сегодняшним одиннадцатиклассникам, завтрашним рабочим, инженерам, учёным предстоит своими руками, используя знания физики и технические достижения, совершенствовать «чудеса» - внося свой вклад в НТП.

9) Модели в механике

 Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.         Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.         Механика вообще подразделяется на три части: статику, кинематику и динамику.         Кинематика (от греческого слова kinema – движение) – раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил.         Динамика (от греческого dynamis – сила) изучает движения тел в связи с теми причинами, которые обусловливают это движение.         Статика (от греческого statike – равновесие) изучает условия равновесия тел. Поскольку равновесие есть частный случай движения, законы статики являются естественным следствием законов динамики и в данном курсе не изучаются.  Механика Галилея и Ньютона называется классической, т.к. она рассматривает движение макроскопических тел со скоростями значительно меньшими, чем скорость света в вакууме,   Для описания движения тел в зависимости от условий задачи используют различные физические модели. Чаще других используют понятия абсолютно твердого тела и материальной точки.   Движение тел происходит под действием сил. Под действием внешних сил тела могут деформироваться, т.е. изменять свои размеры и форму.  Тело, деформацией которого можно пренебречь в условиях данной задачи, называют абсолютно твердым телом (хотя абсолютно твердых тел в природе не существует).  Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.  Можно ли данное тело рассматривать как материальную точку или нет, зависит не от размеров тела, а от условия задачи (например, наше огромное Солнце тоже материальная точка в Солнечной системе).

10) Система отсчета

Система отсчёта — это совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо другихматериальных точек или тел[1].

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями  ,  ,  .

В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п.

10) Траектория, длина пути, вектор перемещения

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

11) Основные кинематические характеристики движения: скорость и ускорение

  Скорость -векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

Ускорение - производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).

12) Нормальное и тангенциальное ускорение

Нормальное — компонент ускорения точки, характеризующая изменение направления вектора скорости для траектории с кривизной. (Вторая компонента,тангенциальное ускорение, характеризует изменением модуля скорости.) Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделенному на радиус кривизны. Термин «центростремительное ускорение» в целом эквивалентен термину «нормальное ускорение»; различия лишь стилистические (иногда исторические).

Тангенциа́льное ускоре́ние  — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие от нормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).

13) Кинематика вращательного движения: угловая скорость и угловое ускорение, их связь с линейной скоростью и ускорением

Часто для наглядного представления движения точки пользуются графиками перемещения, скорости и ускорения в функции от времени в прямоугольных координатных осях.Рассмотрим кинематические графики для равномерного движения. Независимо от того, является оно прямолинейным или криволинейным, мы имеем для него следующие уравнения:

Из этих уравнений следует, что график перемещения равномерного движения является прямой, отсекающей на оси ординат величину s0, т. е. величину перемещения точки в начале движения от начала отсчета (рис.а).

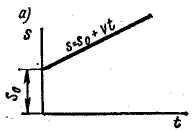
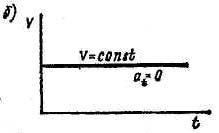
График скорости изображается прямой линией, параллельной оси абсцисс, так как скорость равномерного движения точки — постоянная величина v = const (рис.б).

Рассмотрим кинематические графики для равнопеременного движения. Каким бы ни было это движение — прямолинейным или криволинейным, — для него справедливы уравнения:

График перемещения равнопеременного движения является криволинейным — параболическим, так как он соответствует уравнению параболы (рис. а, б).

На оси ординат эти графики отсекают при t = О величины, соответствующие расстоянию в начале движения от начала отсчетаs0.

График скорости изображается прямой, наклоненной к оси абсцисс (рис. в, г), и отсекает на оси ординат (при t = 0) величину начальной скорости v0.

График ускорения равномерно-переменного движения изображается линией, параллельной оси абсцисс (оси времени) — (рис. д, е.)

При равномерно-ускоренном движении график ускорения располагаем выше оси абсцисс. При равномерно-замедленном движении — ниже (рис. е). При равномерно-замедленном движении значение скорости убывает. Это наглядно видно из (рис. г). Возможен случай, когда скорость, уменьшаясь, достигает нулевого значения (точка М на рис. г). Затем скорость изменяет свой знак и по абсолютному значению начинает увеличиваться. Здесь по существу происходит переход равномерно-замедленного движения в равномерно-ускоренное. Именно такое явление и происходит для случая, изображенного на (рис. б, д) при t = tA, т. е. при изменении алгебраического знака скорости.Между кинематическими графиками существует определенная взаимосвязь. Так, для равномерного движения график скорости изображается линией, параллельной оси абсцисс, а график расстояния — прямой наклонной линией. Для равнопеременного движения график ускорения является прямой, параллельной оси абсцисс, график скорости — наклонная прямая, а график расстояний — параболическая кривая. Эта взаимосвязь графиков следует непосредственно из дифференциальных зависимостей, связывающих ускорение, скорость и расстояние:

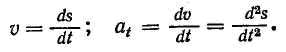
Учитывая аналогию в уравнениях движения точки и уравнениях вращения тела, графическую интерпретацию можно использовать при исследовании вращательного движения, являющегося основным в технике. Здесь вместо расстояния будет фигурировать угол поворота, вместо скорости — угловая скорость, вместо ускорения — угловое ускорение.

14) Масса

Масса-физическая величина, одна из основных характеристик материи, определяющая её инерционные и гравитационные свойства. Соответственно различают М. инертную и М. гравитационную (тяжёлую, тяготеющую).

         Понятие М. было введено в механику И. Ньютоном. В классической механике Ньютона М. входит в определение импульса тела: импульс p пропорционален скорости движения тела v,

         p = mv . (1)

         Коэффициент пропорциональности — постоянная для данного тела величина m — и есть М. тела. Эквивалентное определение М. получается из уравнения движения классической механики

         f = ma . (2)

15) Сила

). Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.^[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление освязанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы

16) Законы Ньютона

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

17) Границы применимости законов Ньютона

До конца прошлого столетия никто не сомневался в абсолютной правильности законов Ньютона. Однако в XX в. выяснилось, что эти законы все-таки не абсолютно точны. Ими нельзя пользоваться, когда тела движутся с очень большими скоростями, которые сравнимы со скоростью света. Альберт Эйнштейн, которого называют Ньютоном XX в., сумел сформулировать законы движения, справедливые и для движения со скоростями, близкими к скорости света. Эти законы лежат в основе так называемой релятивистской механики или теории относительности. А законы Ньютона представляют собой следствие этих законов, когда скорости тел малы по сравнению со скоростью света. Законы Ньютона нельзя применять и при рассмотрении движения внутриатомных частиц. Такие движения описываются законами квантовой механики, в которой классическая механика рассматривается как частный случай. Законы сохранения импульса и энергии, выведенные из законов Ньютона, справедливы и в квантовой механике, и в теории относительности. Механика лежит в основе всего естествознания.

18) Сила трения

Сила, возникающая в месте соприкосновения тел и препятствующая их относительному переме­щению, называется силой трения. Направление силы трения противоположно направлению движения.  Различают силу трения покоя и силу трения скольжения.

Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.

   , где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэф­фициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем.

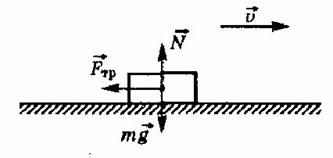
Сила трения скольжения всегда направлена противоположно движению тела. При изменении на­правления скорости изменяется и направление си­лы трения.

Сила трения начинает действовать на тело, когда его пытаются сдвинуть с места.

Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого.

В некоторых случаях трение полезно, в таких случаях трение усиливают. Но в других слу­чаях трение вредно. Например, из-за него изнаши­ваются трущиеся детали механизмов, расходуется лишнее горючее на транспорте и т.д.

Силы трения, в отличие от гравитационных сил и сил упругости, не зависят от координат относительного расположения тел, они могут зависеть от скорости относительного движения соприкасающихся тел. Силы трения являются непотенциальными силами.

Сила трения покоя (υ = 0). 

19) Сила упругости

Сила упругости- сила при деформации тел, и стремящиеся вернуть телу его форму,размеры,объем.

Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации. ,-Закон гука

20) Гравитационная сила

Гравита́ция (всемирное тяготение, тяготение) —фундаментальное взаимодействие в природе, которому подвержены все тела, имеющие массу. Главным образом, гравитация действует в масштабах космоса. Термингравитация используется также как название раздела в физике, изучающего гравитационное взаимодействие.

   — гравитационная постоянная, равная примерно 6,6725×10⁻¹¹ м³/(кг·с²).

- формула

21) Закон всемирного тяготения

2 материальные точки притягиваются друг к другу с силой F, оно пропорциональна массе этих точек и обратно между ними.

22) Использование основного уравнения динамики. Импульс

 импульс механический, мера механического движения; представляет собой векторную величину, равную для материальной точки произведению массы m этой точки на её скорость v и направленную так же, как вектор скорости: p = mv; то же, что Количество движения. Для частицы, движущейся со скоростью, близкой к скорости с света в вакууме, необходимо учитывать зависимость её массы от скорости: 

        где m₀ — масса покоящейся частицы (так называемая масса покоя). В этом случае И. свободной частицы равен  Относительности теория), а связь полной энергии E частицы с её И. даётся соотношением: E = p²c² + m²₀с⁴ Для частицы с нулевой массой покоя (фотон, Нейтрино) р = E/c, такие частицы всегда движутся со скоростью света с.

         И. обладают все формы материи, в том числе электромагнитное (см. Импульс электромагнитного поля) и гравитационное поля. Для полей вводят вектор плотности И. (И. единицы объёма, занятого полем), который выражают через напряжённости полей, потенциалы и т. П

23) Внутренние и внешние силы

Внешние силы—это силы, действующие на тело извне. Под влиянием внешних сил тело или начинает двигаться, если оно находилось в состоянии покоя, или изменяется скорость его движения, или направление движения. Внешние силы в большинстве случаев уравновешены другими силами и их влияние незаметно, только знание законов механики позволяет утверждать о действии внешних сил на тело, находящееся в покое.

Внешние силы, действуя на твердое тело, вызывают изменения его формы, обуславливаемые перемещением частиц.

Внутренними силами являются силы, действующие между частицами, эти силы оказывают сопротивление изменению формы.

Изменение формы тела под действием силы называют деформацией, а тело, претерпевшее деформацию, называют деформированным.

24) Однор́одность пространства 

Однор́одность пространства означает, что нет такой точки в пространстве, относительно которой существует некоторая «выделенная» симметрия, все точки равноправны, поэтому рассматриваемый эксперимент не зависит от нашего выбора точки отсчета. К примеру, измеримпериод колебаний маятника, полученный результат обозначим как Т₁. Теперь перенесем маятник в соседнюю комнату, и проведем то же измерение. Результат запишем как Т₂. Оказывается, что Т₁=Т₂, то есть исход эксперимента не зависит от нашего положения, это и есть проявление однородности пространства.

Однородность — одно из ключевых свойств пространства в классической механике. Пространство называется однородным, если параллельный перенос системы отсчета не влияет на результат измерений.

25)Закон сохранения импульса

Закон сохранения импульса. 

По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить   и  .

Для изменений импульсов тел при их взаимодействии на основании равенства можно записать

,

,

где t — время взаимодействия тел. Из этих выражений получаем

. (16.3)

Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.

Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равенстве нулю суммы действующих сил геометрическая сумма импульсов тел остается неизменной.

Система тел, не взаимодействующих с другими телами, не входящими в эту систему, называется замкнутой системой.

В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса.

Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.

27) Центр масс

        центр инерции, геометрическая точка, положение которой характеризует распределение масс в теле или механической системе. Координаты Ц. м. определяются формулами

          , 

        или для тела при непрерывном распределении масс

         

        где m_к — массы материальных точек, образующих систему, x_k, у_к, z_k — координаты этих точек, М = Σm_к — масса системы, ρ — плотность, V — объём. Понятие о Ц. м. отличается от понятия о центре тяжести (См. Центр тяжести) тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести; понятие же о Ц. м. не связано ни с каким силовым полем и имеет смысл для любой механической системы. Для твёрдого тела положения Ц. м. и центра тяжести совпадают.

28) Закон движения центра масс

Воспользовавшись законом изменения импульса,  получим закон движения центра масс:

                                  dP/dt = M∙dV_c/dt = ΣF_i

Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.

В частности, центр масс замкнутой системы относительно произвольной ИСО движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил.

Внутренние силы не влияют на характер его движения, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе.

Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела - снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила - сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.

29)Момент Инерции

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

30)Теорема Штейнера

Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции   тела относительно произвольной оси равен сумме момента инерции этого тела   относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела   на квадрат расстояния   между осями:

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

31) Кинетическая энергия вращательного движения

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно.

(5.11)

где   - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости   центра инерции тела, и вращения с угловой скоростью  вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

(5.12)

где   - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

32) Момент силы

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело 33) Уравнение динамики вращательного движения твердого тела

второй закон Ньютона для вращательного движения

По определению угловое ускорение   и тогда это уравнение можно

переписать следующим образом

с учетом (5.9)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела  , равно импульсу момента  всех внешних сил, действующих на это тело.

34) Момент импульса

Моме́нт и́мпульса - характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса   материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора иимпульса:

где   — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,   — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп).

35) Закон сохранения момента импульса

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.

36) Деформации твердого тела

Виды деформаций. Деформацией называют изменение формы, размеров тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.

Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, – пластическими.

Различают деформации растяжения и сжатия (одностороннего и всестороннего), изгиба, кручения и сдвига.

Силы упругости. При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

Рис. 5.11.Деформация растяжения (а) и сжатия (б)

Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.

Рассмотрим простейшую деформацию продольного растяжения или одностороннего сжатия. Представим себе однородный стержень длины L, с площадью поперечного сечения S, к концам которого приложены силы F, в результате чего длина стержня меняется на величину ΔL. Для характеристики деформации растяжения существенно не абсолютное значение удлинения стержня ΔL, а относительное удлинение  .

Растягивающие силы считаем положительными; в этом случае (рис. 5.11а) ΔL тоже положительно, поскольку при растяжении длина стержня увеличивается. Сжимающие силы считаем отрицательными; в этом случае (рис. 5.11б) ΔL отрицательно; это означает, что, когда стержень подвергается одностороннему сжатию, его длина L уменьшается.

Эксперименты свидетельствуют, что относительная деформация тем больше, чем больше действующая сила и чем меньше поперечное сечение стержня. Этот результат можно представить в виде математического соотношения

.

(5.1)

Величина   называется механическим напряжением или просто напряжением. С учетом этого выражение (5.1) принимает вид

,

(5.2)

где коэффициент α, носящий название коэффициента упругости, зависит только от материала, из которого сделан стержень.

Наряду с коэффициентом упругости α материал принято характеризовать обратной величиной:

,

(5.3)

которую называют модулем упругости, или модулем Юнга. Подставляя в (5.2) (5.3) получаем:

.

(5.4)

Из выражения (5.4) находим:

.

37) Энергия

Эне́ргия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».

С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.