17.Неоклассическая мультипликативная производств. Ф-ция.

Пр-ная ф-ция наз-ся неоклассической мультипликативной ф-цией, если она непрерывна и удет усл-ям:

1) F(0,L) = F(K,0) =0 - отсутствие одного из ресурсов не обеспечивает результата (продукта) производства;

2) - с ростом объемов ресурсов растет и объем

выпускаемого продукта;

3) - с ростом объемов ресурсов скорость роста

объема продукта снижается;

4) - с неограниченным ростом объема одного из ресурсов выпуск продукта неограниченно растет.

М ультипликативная пр-ная ф-ция явл. степ. ф-цей и задается следующим аналит. выр-ем:

где А - коэффициент технического прогресса; α, β- пок-ли степени пр-ной ф-ции соответственно при ср-вах пр-ва и рабочей силе. Как отмечалось, в частном случае, когда мультипликатив. пр-ная ф-ция называется функцией Кобба - Дугласа.

1 8. Изокванты и изоклины мультипликатив. производств.ф-ции. Изоквантой, или линией уровня на плоскости KOL, наз-ся мн-во точек пл-ти, для кот. F(K,L) – Y₀= const. Для мультипликативной пр-ной ф-ции изокванта имеет вид:

О на предст. степенную гиперболу, асимптотами которой являются оси координат ОК и OL. Для разных значений К и L, кот. формируют точку на конкретной изокванте, объем производимого продукта равняется значению Y₀. Так как на изокванте справедливо равенство , то диф-ал пр-ной ф-ции

Изоклинами наз-ся линии на плоскости KOL наиболее быстрого роста пр-ной ф-ции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке (K, L) задается градиентом

, то уравнение изоклины можно записать

следующим образом:

19. Коэф.Эластич.Производ.Ф-ии от 2х факторов.

Важными хар-ми производ.ф-ии явл. коэф. эластич. выпуска по ресурсам.

Е_К = - 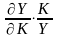Е_L = - 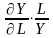Т.е. они равняются отношению предельной производительности соответ. рес-са к его сред.производ-ти.

Коэф. эластич. показывает на сколько % изменится выпуск прод-ции при увеличении затрат одного рес-са на 1 % и сохранении зн-я др.рес-са.

На ряду с понятием эластич.выпуска по затратам рес-сов в эк.анализе применяется понятие эластич. взаимозаменяемости рес-сов. При дв-нии вдоль изокванты F(K,L)=Y₀ =const вместе с координатами (.) (K,L) изменяется зн-е 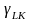, и велечина отношения затрат L/K. Считая,что они связаны функционально: L/K=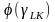 . В предположении,что ф-я дифф-мая,вычислим эластчность:

. Коэф. эластич. взаимозаменяемости рес-сов Е_LK показыв. на сколько % должно измениться отношение затрат рес-сов,чтобы предельная норма заменяемости рес-сов увелич. на 1%.

Е_LK принимает самые различные зн-я на промежутке [0; ). Чем выше зн-е коэф. эластич.взаимозамен.рес-сов,тем в более широких пределах рес-сы могут заменять др.др. При Е_LK =0 возможность замены рес-сов-отсутствует.При Е_LK → рес-сы могут заменять др.в самых широких пределах.