7. Функция спроса по цене.

1)Спрос – это платежеспособная потребность покупателя, т.е. потребность покупателя, располагающего ден. ср-вами для приобретения тов. и усл. Потребность – нуждя человека в благах для поддержания жизнедеятельности и развития личности. На спрос влияют 3 фактора: 1) потребность человека в продукте, 2) цена продукта, 3) уровень ден. доходов потребителя. В условиях рыночного спроса на тов. усл. есть правило: Чем выше цена, тем меньше тех, кто согласиться купить, т.е. уменьшается уровень спроса и наоборот. График имеет вид убывающей кривой

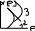1. Со>0, C1>0,α<0,p>0. 2. Со>0, C1<0,α=1. 3. Со<0, C1>0,α>0 (α≠1). Со и С1 – зависят от числа покупателей на рынке, от ден. доходов и вкусов потребителя, от цен конкурентов и цен на замещающие товары. Общее св-во 1, 2, 3 – отрицательное значение x'(p).

8. Построение ф-ий спроса и предложения методом наименьших квадратов.

В качестве исходных данных для построения ф-ии спроса и предложения выступают данные независимого наблюдения предложения и цены. Если необходимо оценить коэфф-ты линейной ф-ии спроса, то применяют непосредственно метод наименьших квадратов p(x)=Co+C1(x). Если нелинейная ф-ия – используют линеаризацию. Самостоятельно применяют метод наим. кВ. для нелинейной ф-ии спроса, т.е. линеаризируют функцию зависящую .

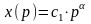9. Эластичность функции.

Эластичностью E_xy(x₀) непрерывной функции y=f(x) в точке x= x₀ называется предел отношения относительного приращения ф-ии в точке x₀ к относительному приращению аргумента в точке x₀, когда абсолютное приращение ∆х→0. Из определения следует, что при малых ∆х: 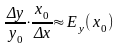, т.е. Эластичность – коэф. пропорциональности м/у относительными изменениями величины ф-ии и аргумента. Показывает на сколько % измениться относительное приращение ф-ии, еслт изменить на 1 % относительное приращение аргумента. Из анализа определения следует:

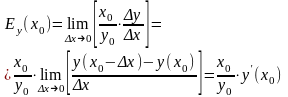
Следовательно, если ф-я y(x) на промежутке (a,b) дифференцируема, то для нее можно вычислить производную в точке х℮(a,b) эластичность

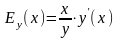
10. Свойства эластичности 1. Пусть даны непрерывные функции Кроме того Тогда для функции ее эластичность Е_y будет удовлетворять следующему условию: Доказательство 2. Пусть функции Тогда эластичность произведения функций y(x)* z(x) равна сумме их эластичностей, а эластичность частного- разности их эластичностей, т.е. Доказательство

3. Пусть дана сложная функция y= y(x), где x= x(t), Тогда эластичность функции y(t) удовлетворяет равенству Доказательство 4. Пусть для функции y=f(x) существует обратная функция x= g(y). тогда эластичность обратной функции удовлетворяет соотношению:

Доказательство Поскольку для обратной функции выполняется тождество f(g(y))=y, тоб применяя cв-во 3 получим

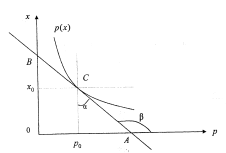
11.Эластичность функции спроса и предложения. Эластичность ф-ции предл-я. Рассмотрим график ф-ции предл-я p=p(x) и эластичность E_p в точке x=x₀.

Эластичность E_p в точке x=x₁: Т.о. с учетом геом. смысла производной геом. смысл эл-ти – отн-е длины касательной от точки касания до точки пересечения касательной с осью ординат к длине касательной от точки пересечения с осью абсцисс.Из привед. примеров геом. смысла, эластичн-ти ф-ции предл-я след-ет, что С эк. точки зрения предл-е счит. эластичным (Е_р > I), если изм. рын. цены товара на опред. вел. в % влечет за собой более значит. в % изм-е объема пр-ва и предложения данного товара.Е_p=1 соотв. случаю, когда изм-е рын. цены товара на опред. величи­ну в % влечет за собой такое же в % изм-е объема пр-ва и предл-я товара. Неэластичным считается предл-е, если изм-е рын. цены на 1% вызывает изм-е объема пр-ва менее чем на 1% (0 < Е_р <1).

Эл-ть ф-ции спроса. Рассмотрим грфик ф-ции спроса x= x(p). где x(p)- спрос, a p- цена. Из гр-ка след., что чем выше цена p, тем меньше спрос x=x(p). Согласно геом. смыслу пр-ной:

А налогично, как для ф-ции предл-я, можно показать, что эл-ть ф-ции спроса находится в пределах , поскольку перед отн-ем длин стоит знак минус. Различ. след. виды эл-ти спроса по цене: эл-ть единичная, эластичный спрос, неэластичный спрос, совершенно эла­стичный спрос, совершенно неэластичный спрос. Под единичной эл-тью понимают случай, когда Е_х=-1 то есть когда на каждый % изм-я цены спрос количественно изм-ся на 1 %. При эл. спросе (Е_x<-1) величина спроса изм-ся в большей мере, чем цена, и, наоборот, при неэластичном спро­се (-1 < Е_х < 0). Совершенно эластичный спрос определяет сит-ю, при кот. величина спроса бесконечно изм-ся - при малом измене­нии цены (Е_х=--00). Совершенно неэластичный спрос (Е_х = 0) обуслов­ливается ситуацией, когда величина спроса не изменяется при любом изменении цены. Необходимо заметить, что величина выручки будет определяться ви­дом эл-ти и характером изм-я цены. В табл. представлены изменения выручки в зав-ти oт знака изм-я цены и вида эл-ти спроса.