1. Абсолютные и относительные величины в экономическом анализе.

Абсолютные – хар-ют объмные или денежные размеры экономич. показ-лей. Дают представление о запасах сырья, материала, размерах перевозимого груза, объемах ден. ср-в. Бывают: 1) Натуральные – экон. пок-ли в натурально вещественной форме, выражаютя в длине, массе, объеме, мощности, число построенных домов. 2) Трудовые ед. – чел/час, чел/день, чел/год. 3) Стоимостные – руб, доллар, евро – характеризуют ВВП, доход, расход, величины ОС, издержки пр-ва и т.д. Относительные – отношение абсолютных или других относительных величин и выражают кол-во единиц одного показателя на единицу другого. Вел-нп с кот. производится сопоставление (знаменатель) наз-ся базисной. Выражаются в безразмерных коэффициентах, % или в единицах присущих соотносимым абсолютным величинам. Различают: 1) Интенсивности – в результате сопоставления разноименных, связанных м/у собой абс. величин на момент или харак-ют степень развития экономического явления. 2)Динамики – хар-ют изменение во времени плановых заданий и относительных величин интенсивности. 3) Выполнения плана – для контроля за ходом выполнения планов. Вычисляются как отношение фактического уровня абс. или отн. вел-ны к плановым их значениям. 4) Сравнения – хар-ют сравниетельные размеры одноименных величин в одинаковый период времени, но к разным объектам. 5) Структуры – хар-ют доли отдельных частей в целом.

2. Суммарные, средние и предельные величины в экономич. Анализе.

1) Суммарные вел-ны в эк-ке – абсолютные вел-ны ли вел-на, для кот. существует средняя или предельная вел-на. Она рассматривается как функция F(x), ф-я м.б. аналитической или табличной. Также суммарн. вел-на в эк-ке – доход или издеожки как ф-ии объема перевозимого груза; объем перевозимого груза как ф-я ресурсов, в качестве кот-х выступает труд и капитал и др. 2) Средняя величина – опр-ся как отношение суммарной величины к независимым переменным 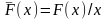.Пример – средняя фондоотдача, ср. доход, ср. грузооборот. 3) Предельная (маржинальная) вел-на – опр-ся как производная суммарной вел-ны F(x) по независимой переменной х: MF(x)=F'(x) – когда х непрерывна. Если суммарная вел-на меняется дискретно, то MF(x) – это отношение изменения ∆F(x) суммарной вел-ны F(x) к вызвавшему это изменение приращению ∆х независимой переменной х: MF(x)= ∆F(x)/ ∆х.

3. Общая характеристика математических функций, используемых в экономике.

Функция – это правило по которому одной величине х из множества Х соответствует другая вел-на у из мн-ва Y. х – переменная или аргумент, y – ф-я или зависимая переменная. В экономике: х – фактор, объясняющая вел-на, у – результатирующая или объясняемая вел-на. В эк-ке большое число ф-ий: -производственная (результатирующая вел-на – это объем пр-ва, а фактор – это ресурсы, капитал, труд), -издержек пр-ва, -дохода, -полезности, -спроса, -предложения, -непрерывных % и т.д. Ф-ии для описания связи 2-х элементов: 1) линейная y=a+bx, 2) квадратичная y=ax²+bx+c, 3)кубическая y=ax³+bx²+cx+d, 4) обратнопропорц. y=a-b/x (x≠0), 4)показательная y=a^x. 5) степенная – y== a · x^b. Пример: 1) Ф-я потребления энергии y от объема производимой продукции (x) – это линейная ф-я y=a+bx. Если разделить на x, то получим y/x=a/x+b=z – это выражение зависимости удельного расхода электроэнергии на ед. прод-ии z в зависимости от объема выпущенной прод-ии x в виде уравнения равносторонней гиперболы. 2) В эк-ке часто примен. многочлен 2ой степени y=ax²+bx+c. При определении x (аргумента) – график м.б. симметричен, это ф-ии описывают – з/п работников физического труда под возрастом, зависимость урожаемости от кол-ва внесенных удобрений. Кривая Филипса – хар-ет нелинейную зависимость м/у нормой безработных и % прироста з/п y=a+b/x. Кривая Эйнгеля – сформулировал закономерность согласно которой с ростом дохода, доля его расходуемого на продовольствие уменьшается y=a-b/x, у – доля на продовольствие.