1)ВП - последовательность сменяющих друг друга состояний некоторой информационной среды.

Модель ВП – описание последовательной смены состояний определенной среды.

• Теоретическая: математическая, схема(алгоритм)

• Компьютерная программа

Виды ВП

Общий случай	Частный случай
параллельные	последовательные
с автопараллельностью	без автопараллельности
двумерные	одномерные
общего вида	приведенные

Методы организации управления ВП:

• последовательное управление (ПУ)

• последовательно-параллельное управление (ППУ)

• асинхронное управление (АУ)

2) Проблема разрешимости

• Тезис Тьюринга: функция F является (частично) вычислимой, если существует машина Тьюринга Т такая, что FT = F. Говорят также, что для функции F существует (частичный) алгоритм вычисления ее значений, задаваемый машиной Т.

• Пусть V – алфавит, М ÍV – множество слов в V.

FM - Характеристическая функция

FM(а) = 1, если а ÎМ, и FM(а) = 0, в остальных случаях.

Множество М называется разрешимым, если его характеристическая функция вычислима.

• Теорема (Тьюринг). Проблема остановки машины Тьюринга неразрешима.

3) АП

• АП=<S, F, I, R>

• S={“события, организующие процесс”}

• FÍSxS

• I ={“инициаторы”}; I ÍS

• R={“результанты”}; R ÍS

Способы задания АП

• Описание множеств списками

АП=<S,F>

S={s1, s2, s3, s4, s5, s6};

F={(s1,s3); (s1,s4); (s2,s1); (s3,s5); (s5,s1); (s4,s6)}

ИЛИ

Таблица функции следования

Матрица смежности ортграфа

Диаграмма ортграфа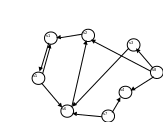

• Назначение инициаторов:

• 1) ("iÎ I) [$sÎ S: iFs].

• 2) ("iÎ I) [Ø($sÎ S\I): sFi].

• Назначение результантов:

• 1) ("rÎ R) [$sÎ S: sFr].

• 2) ("rÎ R) [Ø($sÎ S\R): rFs].

Граф- Совокупность двух множеств: множества точек (вершин) V и множества линий (ребер)Е ÍVxV. Е={(vi,vj)| vi,vj ÎV}.

4) Эффективный ап, классы эквивалентности, управляемый ап.

• Эффективный процесс

Определение: АП называется эффективным, если

1. из его инициаторов все траектории ведут в результанты

2. каждая из траекторий, приводящих к результанту, начинается в некотором инициаторе

3. процесс не содержит ориентированных циклов вне множества R результантов.

Эффективность АП оставляет место недетерминизма, т.е. возможно, что из одного инициатора процесс попадает в разные результанты.

1. Если I={s1, s5}, R={s4}, то не выполняется свойство 1;

2. если I={s7}, R={s1,s2, s3, s4, s5, s6}, то не выполняется свойство 2;

3. если I={s7, s8}, R={s4}, то не выполняется свойство 3;

4. если I={s7, s8}, R={s1, s2, s3, s4, s5, s6}, то асинхронный процесс эффективный.

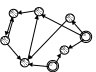классы ап эквивалентности: если есть инициатор начальный, рез-тант заключительный. Если есть ф. следования яв-ся взаимно однозачн событ то процесс детерменирован

• Управляемый процесс

Определение: Если в эффективном АП каждая допустимая последовательность классов ведёт из начального класса в один и только один заключительный класс, то такой процесс называется управляемым.

В управляемом процессе вводится ограничение на степень недетерминизма: для каждого инициатора, все траектории, из него исходящие ведут в один заключительный класс.

П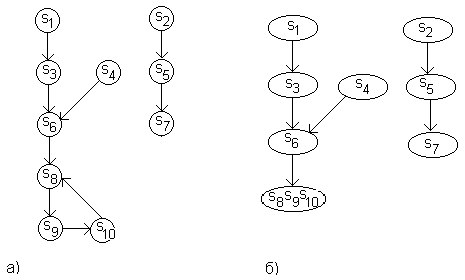 ример:

5) Простой ап, его протокол. Репозиция ап.

• Простой процесс

Определение: Эффективный АП называется простым, если он удовлетворяет условиям:

1. " iÎ I i F s Þ sÏ I

2. " rÎ R s F r Þ sÏ R

Репозицией АП Р={S, F, I, R} называется эффективный асинхронный процесс P`={S`,F`,I`,R`}, где S`=I U R U Sд, I`Í R, R`Í I.

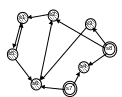
Если I`=R, R`=I, то репозиция называется полной, иначе частичной.

Протокол простого АП отношение QÍI*R на каждой траектории процесса один рез-тант и инициатор