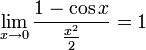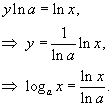- •1.Квадратные матрицы и их свойства. Определители и их свойства, вычесление определителей второго и третьего порядка. Минор и алгебраическое дополнение.
- •2.Системы линейных алгебраических уравнений. Правило Крамера. Метод Гаусса.
- •4.Теорема Кронека-Капелли. Решение систем алгебраических уравнений матричным способом.
- •5. Собственное значение и собственные векторы матрицы.
- •6. Определение вектора. Модуль вектора. Определение компланарных, коллинеарных и равных векторов.
- •7. Проекция вектора на ось. Разложение вектора на ось по единичным векторам.
- •8. Умножение вектора на число. Сложение и вычитание вектора.
- •9. Расстояние между двумя точками в прямоугольной системе координат. Деление отрезка в данном отношении.
- •10. Скалярное произведение 2-х векторов и его свойства. Угол между 2-мя векторами.
- •11. Векторное произведение. Его свойства. Площадь δ и s.
- •12. Формулы векторного произведение векторов, заданных проекциями. Условие коллинеарности векторов.
- •Смешанное произведение 3-х векторов. Геометрическое толкование. Признак компланарности 3-х векторов.
- •Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.
- •Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.
- •Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.
- •14.Уравнение прямой с угловыми коэффициентом и проходящие через заданную точку.
- •15.Уравнение прямой, проходящей через две заданные точки
- •16. Общее уравнение прямой линии. Угол между двумя прямыми.
- •17. Полярная система координат на плоскости.
- •18. Нормальное уравнение прямой. Расстояние от данной точки до данной прямой.
- •19. Окружность, ее каноническое и общее уравнение
- •20.Эллипс. Вывод канонического уровнения эллипса, его характеристики.
- •21. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
- •22. Прямая на плоскости. Виды уравнений прямой на плоскости. Угол между двумя прямыми.
- •23. Эллипс. Определение. Вывод канонического уравнения.
- •24. Гипербола. Определение. Вывод канонического уравнения.
- •25.Переменные и постоянные величины множества. Функции. Область определения, способы задания. График функции. Приращение функции.
- •26.Предел переменной величины (последовательности). Предел функции при непрерывном стремлении аргументы к конечному значению или к бесконечности. Свойства функций, имеющих предел.
- •28.Теоремы о пределах суммы, произведения и частного, признаки существования предела: а) для монотонной ограниченной последовательности; б) для функции, заключенной между двумя функциями.
- •29.Первый замечательный предел.
- •30.Второй замечательный предел. Натуральные логарифмы. Применение замечательных пределов к нахождению функции.
- •32.Производная, ее геометрический и механический смысл. Касательная и нормаль к плоскости кривой. Дифференцируемость функций.
- •33.Производная суммы, произведения и частного. Гиперболические функции, их свойства и графики.
- •34. Производные основных элементарных функций (степенных, логарифмических, показательных и гиперболических функций). Производная сложной и обратной функции. Производные тригонометрических функций.
- •Производная обратной функции
- •Производная сложной функции
- •Производные тригонометрических функций
- •Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.
- •36. Функции заданные параметрическими уравнениями их дифференцирование. Теоремы Коши, Лагранжа, Роля. Правило Лопиталя.
- •38. . Экстремумы функции. Необходимый признак экстремума. Достаточный признак экстремума, использующие первую и вторую производную.
- •39. Исследование условий и построение графиков.
- •40.Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры. Вертикальная
- •[Править]Горизонтальная
- •[Править]Наклонная
- •[Замечание
29.Первый замечательный предел.
1 замечательный предел.
![]()

Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда

Разделим все на
![]() и
получим:
и
получим:

Т.к.
![]() ,
то по признаку существования пределов
следует
.
,
то по признаку существования пределов
следует
.
Следствия
Примеры.
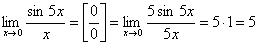 .
.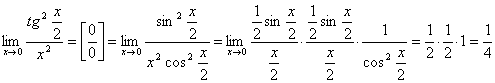 .
.
30.Второй замечательный предел. Натуральные логарифмы. Применение замечательных пределов к нахождению функции.
Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом
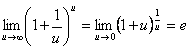
Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).
![]()
Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

Если x→∞, то n→∞, тогда

По признаку о существовании пределов:
Следствия
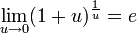
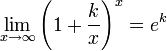
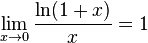
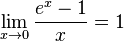
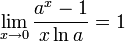 для
для 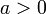 ,
, 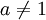
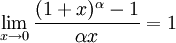
Примеры.
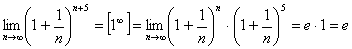 .
.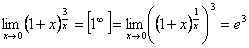 .
.
Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.
Соотношение между логарифмом по основанию a и натуральным логарифмом
Пусть число a является основанием логарифма (a > 0, a ≠ 1), и пусть задана логарифмическая функция
Отсюда следует, что
Взяв натуральный логарифм от левой и правой части, получаем
Последняя формула выражает произвольный логарифм числа x по основанию a через натуральный логарифм этого числа. Полагая x = e, можно записать
Если a = 10, то получаем десятичный логарифм:
Обратное соотношение имеет вид:
![]()
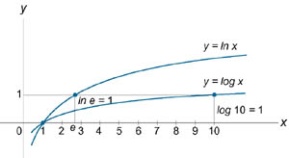
Графики функций y = ln x и y = lg x показаны на рисунке 1.
|
|
|
Рис.1 |
|
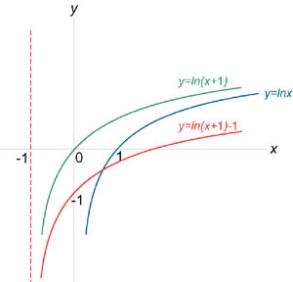
Рис.2 |
31.Непрерывность функции в точке. Непрерывность суммы, произведения, частного. Односторонние пределы. Односторонняя непрерывность. Точки разрыва функции их классификация. Непрерывность элементарных функций. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего, наименьшего значений, существование промежуточных значений.
Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:
![]()
Это означает:
- функция определена в точке х0 и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
Точки разрыва функции – это точки в которых нарушается непрерывность функции.
Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)
 и
и

При этом, если:
- А1=А2 то точка х0 называется точкой устранимого разрыва;
- А1≠А2 то точка х0 называется точкой конечного разрыва.
|A1 – A2| называется скачком функции.
Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.
Непрерывность действительной функции в точке
1) ! точка х0 принадлежит области задания функции f(x) и любая е-окрестность точки х0 содержит отличные от х0 точки области заданной функции.
Определение. Функция f(x) называется непрерывной в точке х0, if предельное значение этой функции в точке х0 существует и =частному значению f(х0).
Условие непрерывности функции f(x) в точке а: lim(/x->a)f(x)=f(x0)
2) Приращение функции y=f(x) в данной точке x0 называется разность (delta)y=f(x0+(delta)x)-f(x0), где (delta)х – приращение аргумента.
Определение. Функция у=f(x) называется непрерывной в точке x0, if это функция определена на какой-нибуть окрестности точки x0 и iflim(x->0)(delta)y=0 т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Непрерывность суммы и произведения непрерывных функций.
Арифметические операции над непрерывными функциями приводят к непрерывным функциям.
Теорема. ! заданные на одном и том же множестве функции f(x) и g(x) непрерывны в точке х0. Тогда функции f(x) ±g(x), f(x)*g(x) и f(x)/g(x) непрерывны в точке х0 (частное условие при g(х0) ≠0)
Доказательство. Так как непрерывные в точке x0функции f(x) и g(x) имеют в этой точке предельные значения f(x0) и g(x0), то по теореме о пределах функций (гласит о том, что, если функции f(x) и g(x) имеют в точке x0 предельные значения В и С, то функции f(x)±g(x), f(x)*g(x) иf(x)\g(x) (при C ≠0) имеют в точке x0 предельные значения, равные соответственно B±C, B*C и B\C) предельные значения функций f(x)±g(x),f(x)*g(x) и f(x)\g(x) существуют и соответственно равны f(x0)±g(x0), f(x0)*g(x0) и f(x0)\g(x0). Эти величины как раз равны значениям соответствующих функций в точке x0. Следовательно, согласно Определению 1 эти функции непрерывны в точке x0.
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.
Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.
Т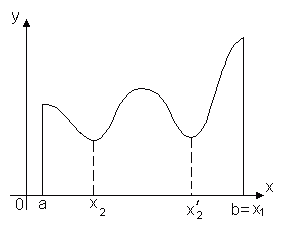 еорема
утверждает, что если функция y
= f(x) непрерывна
на отрезке [a, b],
то найдётся хотя бы одна точка x1 [a, b]
такая, что значение функции f(x) в
этой точке будет самым большим из всех
ее значений на этом отрезке: f(x1)
≥ f(x). Аналогично
найдётся такая точка x2,
в которой значение функции будет самым
маленьким из всех значений на отрезке: f(x1)
≤ f(x).
еорема
утверждает, что если функция y
= f(x) непрерывна
на отрезке [a, b],
то найдётся хотя бы одна точка x1 [a, b]
такая, что значение функции f(x) в
этой точке будет самым большим из всех
ее значений на этом отрезке: f(x1)
≥ f(x). Аналогично
найдётся такая точка x2,
в которой значение функции будет самым
маленьким из всех значений на отрезке: f(x1)
≤ f(x).
Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2'.
Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.
Также теорема перестаёт быть верной для разрывных функций. Приведите пример.
Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.
Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать. Эта теорема допускает следующее обобщение. Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C. Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C. Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности: Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями. |
|