18. Нормальное уравнение прямой. Расстояние от данной точки до данной прямой.

Нормальное уравнение прямой

где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель , взятый со знаком, противоположным знаку свободного члена C.

Расстояние от данной точки до данной прямой

Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую. Она определяется по формуле

Правило. Чтобы определить расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:

Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.

Отклонение данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.

19. Окружность, ее каноническое и общее уравнение

Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности

Каноническое уравнение окружности (x-x₀)²+(y-y₀)²=R².

В уравнение окружности (x – a)² + (y – b)² = R², где (a; b) — координаты центра, а R — радиус окружности.

20.Эллипс. Вывод канонического уровнения эллипса, его характеристики.

- Элипс.

Определение. Эллипсом называется ГМТ плоскости сумма расстояний которых до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.

Определение. Расстояние от произвольной точки М плоскости до фокуса эллипса называется фокальным радиусом точки М.

- Каноническое уравнение эллипса.

Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:

Для определённости положим, что В этом случае величины и — соответственно, большая и малая полуоси эллипса.

Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:

Координаты фокусов эллипса:

Эллипс имеет две директрисы, уравнения которых можно записать как

Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен

Фокальные радиусы, т. е. расстояния от фокусов до произвольной точки кривой

Уравнение диаметра, сопряжённого хордам с угловым коэффициентом :

Уравнение касательной к эллипсу в точке имеет вид

Условие касания прямой и эллипса записывается в виде соотношения

Уравнение касательных, проходящих через точку

Уравнение касательных, имеющих данный угловой коэффициент :

Уравнение нормали в точке

• Характеристики

Форма эллипса зависит от отношения b/a . При b=a эллипс превращается в окружность, уравнение эллипса (11.7) принимает вид x²+y²=a². В качестве характеристики формы эллипса чаще пользуются отношением . Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и o6oзначается буквой ε («эпсилон»):

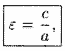(11.8)

причем 0<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу (11.8) можно переписать в виде

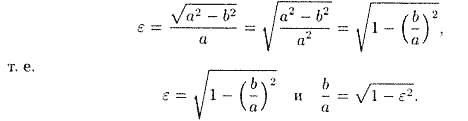
Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.