8. Умножение вектора на число. Сложение и вычитание вектора.

Произведение ненулевого вектора на число - это вектор, коллинеарный данному, а его модуль равен модулю данного вектора, умноженному на модуль числа.

Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Так в случае плоской задачи произведение вектор на a = {a_x; a_y} на число b находится по формуле a ·b = {a_x · b;a_y · b}

Так в случае пространственной задачи произведение вектора a = {a_x;a_y;a_z} на число 

b находится по формуле 

a ·b = {a_x · b;a_y · b;a_z · b}

При сложении двух векторов   суммарный вектор   представляет собой диагональ параллелограмма, построенного на векторах   и   как на сторонах (начала всех трех векторов должны совпадать). По этому же правилу производится операция вычитания векторов

Проекции результирующего вектора на координатные оси при сложении векторов равны алгебраической сумме проекций слагаемых векторов

При вычитании векторов проекции результирующего вектора равны разности проекций векторов   и 

9. Расстояние между двумя точками в прямоугольной системе координат. Деление отрезка в данном отношении.

Расстояние d между двумя точками M1(x1,y1,z1) и M2 (x2,y2,z2) в пространстве определяется формулой

К оординаты x, y, z точки М, которая делит отрезок MM1, ограниченный точками M1(x1,y1,z1) и M2 (x2,y2,z2), в отношении ,определяется по формулам:

В частности, при имеет координаты середины данного отрезка:

10. Скалярное произведение 2-х векторов и его свойства. Угол между 2-мя векторами.

Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

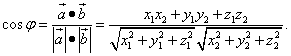Угол между 2-мя векторами.

11. Векторное произведение. Его свойства. Площадь δ и s.

Векторным произведением вектора на вектор называется вектор , который:

1. Перпендикулярен векторам и .

2. Имеет длину, численно равную площади параллелограмма, образованного на векторах и .

, где

3. Векторы , и образуют правую тройку векторов.

Свойства:

1. 

2. 

3. 

4. 

Векторным произведением вектора на вектор называется вектор, обозначаемый символом и

определяемый следующими тремя условиями:

1). Модуль вектора равен , где - угол между векторами ;

2). Вектор перпендикулярен к каждому из вектора и ;

Векторное произведение зависит от порядка сомножителей, именно:

Модуль векторного произведения равен площади S параллелограмма, построенного на векторах и :

Само векторное произведение может быть выражено формулой ,где - орт векторного произведения.

Векторное произведение обращается в нуль тогда и только тогда, когда векторы а и b коллинеарны. В частности, .

Если система координатных осей правая и векторы и заданы в этой системе своими координатами:

т о векторное произведение вектора на вектор определяется формулой