[Замечание

В обозначениях Лейбница цепное правило для вычисления производной функции   где   принимает следующий вид:

     Определение. Производная от функции z=f(x,у) по х, найденная в предложении, что у остается постоянным, называется частной производной от z по х и обозначается   или f'_x (x,у). Аналогично определяется и обозначается частная производная z по у.      Если функция z=f(x,у) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть представлено в виде:        ,                                             (1)      где   при  .

Производная неявно заданной функции

Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале ]a, b[, то во многих случаях ее производную можно найти из уравнения

ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ ПЛОСКОСТИ К ПОВЕРХНОСТИ

Касательной плоскостью к поверхности   в её точке M0  называется та плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности через точку

Вектор 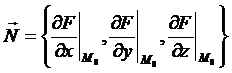  называется вектором нормали к  поверхности в точке М₀.

Нормалью к поверхности в точке   называется прямая, проходящая через эту точку и имеющая направление вектора  .

Уравнение касательной плоскости к поверхности составляем как уравнение плоскости, проходящей через точку  и имеющей известный нормальный вектор:

(3)

Канонические уравнения нормали к поверхности   в ее точке   имеют вид:

(4)

Оба уравнения составлены как известные из аналитической геометрии уравнения плоскости и прямой в пространстве.

Пример (составления уравнений касательной плоскости и нормали к поверхности)

Составить уравнение касательной плоскости и нормальной прямой к поверхности   в её точке  .

Решение

            ,  ,  .

В точке   будет  ,  ,     вектор нормали  .

Уравнение касательной плоскости: ;

уравнение нормали:   .

Ответ:   ;  .

Замечание

Если в точке М₀, принадлежащей поверхности  , все  = = =0, то вектор нормали к поверхности равен ноль-вектору; если хотя бы одна производная  ,  ,   не существует, то вектор нормали не существует.

Точки, в которых вектор нормали к поверхности равен ноль-вектору или не существует, называются особыми точками поверхности. Касательная плоскость к поверхности в таких ее точках не существует.

Определение 1. Касательной плоскостью к поверхности   в данной точке P (x₀, y₀, z₀) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.

Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка  P (x₀, y₀, z₀) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р.

Пусть х = х(t), у = у(t), z = z(t) –  параметрические уравнения линии L.

Предположим, что: 1) функция F(х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю; 2) функции  х(t),у(t), z(t) также дифференцируемы.

Поскольку кривая принадлежит поверхности s , то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [x(t), у(t), z (t)] = 0.

Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и в точке P (x₀, y₀, z₀):

.

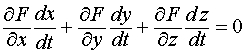Пусть точке Р соответствует значение параметра t₀, то есть x₀ = x (t₀), y₀ = y (t₀),    z₀ = z (t₀). Тогда последнее соотношение, вычисленное в точке Р, примет вид

.                  (17)

Формула (17) представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор

,

не зависящий от выбора кривой на поверхности   .

Второй вектор  –  касательный в точке Р к линии L, а значит, зависящий от выбора линии на поверхности, то есть является переменным вектором.

П ри введённых обозначениях равенство (17) перепишем как  . Его смысл таков: скалярное произведение равно нулю, следовательно, векторы   и   перпендикулярны. Выбирая всевозможные кривые (см. рис. 54), проходящие через точку Р на поверхности s , мы будем иметь различные касательные векторы, построенные в точке Р к этим линиям; вектор же   от этого выбора не зависит и будет перпендикулярен любому из них, то есть все касательные векторы

расположены в одной плоскости, которая, по определению, является касательной к поверхности s , а точка Р в этом случае называется точкой касания. Вектор   является направляющим вектором нормали к поверхности.

Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:

;         (18)

(18) – уравнение касательной плоскости, построенной в точке P (x₀, y₀, z₀) к поверхности s , заданной уравнением F(х, у, z) = 0;

;              (19)

43. Часные производные и дифференциал высших порядков. Необходимое и достаточное условия существование экстремума функций двух переменных. Наибольшее и наименьшее значение функции. Условные экстремумы. Метод множителей Лагранжа.

Производные высших порядков.

Рассмотрим функцию   , определенную на некотором промежутке    . Вычислим производную  , которая также является функцией на  . Производной второго порядка от функции   называется производная от ее производной:    . Аналогично определяют производную любого порядка:   .

ПРИМЕР 1.  Вычисление производных высших порядков

Дифференциалы высших порядков.

Рассмотрим дифференциал функции   в произвольной точке промежутка  :  . Здесь   - приращение независимой переменной, которое является числом и не зависит от  . Сам же дифференциал есть функция от  , и можно вычислить дифференциал от этой функции:    При   этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле  Аналогично вычисляется дифференциал любого порядка  .

ПРИМЕР 2.  Вычисление дифференциалов высших порядков

Понятие инвариантности формы дифференциала.

Рассмотрим дифференциал функции   в произвольной точке промежутка  :  . Здесь  - приращение независимой переменной, которое является числом и не зависит от  . Пусть теперь    - функция независимого переменного  , определенная на промежутке   . Тогда   - сложная функция переменного  . Вычислим ее дифференциал, используя формулу дляпроизводной сложной функции:  . Заметим, что  и выражение для дифференциала принимает ту же форму  , хотя здесь   уже функция переменного   . Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что   - функция переменного   . Поэтому  и форма второго (а также и всех следующих) дифференциала неинвариантна.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция   достигает экстремума при  , то каждая частная производная первого порядка от   или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   функция   имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка   является критической точкой функции  , т.е. , тогда при  : 1)   имеет максимум, если дискриминант   и  , где 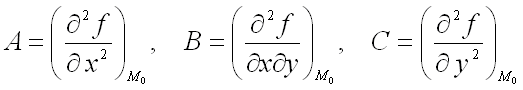 ; 2)  имеет минимум, если дискриминант   и  ; 3)   не имеет ни минимума, ни максимума, если дискриминант  ; 4) если   , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Наибольшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  . Наименьшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  . Эти определения интуитивно понятны: наибольшее (наименьшее) значение ф ункции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе  .

Условным экстремумом функции z = f(x, y) называется экстремум этой функции, в том случае, когда переменные х и у связаны уравнением           (х, у) = 0 (уравнение связи).

Нахождение условного экстремума можно свести к исследованию на обычный экстремум функции Лагранжа

 

                                    F(x,y) = f(x, y)  +  (x,y),                                      (4)                                    

 

где   – некоторый постоянный множитель.

Необходимые условия экстремума функции Лагранжа имеют вид

 

                                                                            (5)

Из этой системы трех уравнений можно найти неизвестные х, у и . Вопрос о существовании и характере условного экстремума решается на основании  знака второго дифференциала функции Лагранжа

 

 

для всех решений системы (5) при условии, что дифференциалы переменных dx и dy  связаны уравнением

 

      .