38. . Экстремумы функции. Необходимый признак экстремума. Достаточный признак экстремума, использующие первую и вторую производную.

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство (f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ^'(x)  0

(f ^' (x)  0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) ≤ f(x_о) (f(x) ≥ f(x_о)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ^'(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ^' (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную f ^' (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f ^' (x_о) = 0, >0 ( <0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

39. Исследование условий и построение графиков.

- найти область определения функции

- найти точки пересечения графика с осями координат

- найти интервалы знака постоянства

- исследовать на четность, нечетность

- найти асимптоты графика функции

- найти интервалы монотонности функции

- найти экстремумы функции

- найти интервалы выпуклости и точки перегиба

40.Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры. Вертикальная

Вертикальная асимптота — прямая вида   при условии существования предела  .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

[Править]Горизонтальная

Горизонтальная асимптота — прямая вида   при условии существования предела

.

[Править]Наклонная

Наклонная асимптота — прямая вида   при условии существования пределов

Пример наклонной асимптоты

1. 

2. 

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен  ), то наклонной асимптоты при  (или  ) не существует!

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела  , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при  , и из выше указанных замечаний следует, что

1. Функция имеет или только одну наклонную асимптоту, или одну вертикальную асимптоту, или одну наклонную и одну вертикальную, или две наклонных, или две вертикальных, либо же вовсе не имеет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

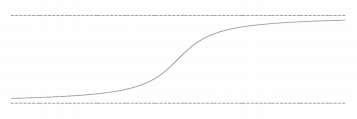
График функции с двумя горизонтальными асимптотами

]Нахождение асимптот

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов 

3. Нахождение двух пределов  :

если   в п. 2.), то  , и предел   ищется по формуле горизонтальной асимптоты,  .

[править]Наклонная асимптота — выделение целой части

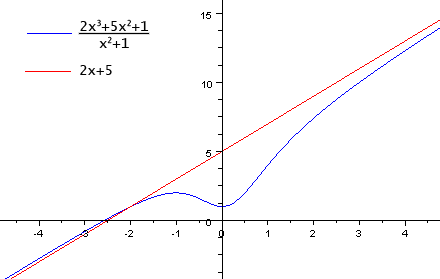
Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция  .

Разделив нацело числитель на знаменатель, получим:

.

При    ,    ,   то есть:

,

и   является искомым уравнением асимптоты.

[править]Свойства

• Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости^[4]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.

Общая схема исследования функции и построения её графика

После того как мы обсудили многие аспекты поведения функции и способы их исследования, сформулируем общую схему исследования функции. Эта схема даст нам практический способ построения графика функции, отражающего основные черты её поведения.

Пусть дана функция  . Для её исследования нужно:

1). Найти её область определения  . Если это не слишком сложно, то полезно найти также область значений  . (Однако, во многих случаях, вопрос нахождения   откладывается до нахождения экстремумов функции.)

2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси  ), не является ли она периодической.

3). Выяснить, как ведёт себя функция при приближении аргумента   к граничным точкам области определения  , если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции. Поясним сказанное примером:

        Пример 7.36   Пусть   Эта функция определена на всей числовой оси, однако 0 является точкой разрыва функции: при   функция стремится к  . Значит, вертикальная прямая   служит вертикальной асимптотой функции, хотя функция и определена в точке  .     

4). Если область определения   вклоючает в себя лучи вида   или  , то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при   или   соответственно.

5). Найти точку пересечения графика с осью   (если  ). Для этого нужно вычислить значение  . Найти также точки пересечения графика с осью  , для чего найти корни уравнения   (или убедиться в отсутствии корней). Уравнение   часто удаётся решить лишь приближённо, но уже отделение корней¹⁹ помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

6). Найти интервалы монотонности функции   (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной  .

На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

7). Найти интервалы выпуклости и вогнутости функции. Это делается с помощью исследования знака второй производной  . Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.

8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график.

41. Определение функции нескольких переменных. Геометрическое изображение функции двух переменных. Частное и полное приращение функции. Граница и непрерывность функции. Частные производные функций нескольких переменных. Полное приращение и полный дифференциал.

Если каждой паре 2-х независимых переменных (х;у) є Д из области Д можно поставить во взаимное однозначное соответствие некоторого значения z, то z называется функцией 2-х переменных. Z=f(x;y)

Геометрическое изображение функции 2-хпеременных:

Задана функция z=f(x;y) и область определения функции (х;у) є Д тогда геометрическое изображение Z называется совокупностью точек Р(х;у), координаты которых удовлетворяют исходному z=f(x;y).

Геометрическим аналогом функции 2-х переменных есть некоторая поверхность в пространстве проэктирующаяся на плоскости ОХУ в области определения Д.

Частное преращение функции:

Пусть задана функция z=f(x;y), предложим, что у=константа, а х получило преращение в Δх, тогда рассмотрим соответственное преращение функции

F(x+Δx,y)-f(x,y)= ΔxZ это называется частным преращением функции по переменной х.

Аналогично получаем частное преращение по переменной у.

Полное преращение функции:

Δz=f(x+Δx,y+Δy)-f(x,y) при чем Δz не равна ΔxZ+ΔyZ

Аналогично находим частное и частное преращение для функции числа переменных.

Непрерывность функции:

Пусть т.М0(х0,у0) є Д функции z=f(x,y) тогда функция z=f(x,y) является неприрывной в т.М0, если выполняется равенство lim f(x,y)=f(x0,y0) где х и у стремятся к х0 и у0 – в этом случае функция называется непрерывной в т. М0(х0,у0)

Существует и 2-ое определение непрерывности:

LimΔz=0 Δx и Δу стремятся к 0

Функция непрерывна в каждой точке области, является непрерывной во всей области.

Частные производные функций нескольких переменных:

Частные производные функции z=f(x;y) по переменной х, называется придел отношения частного преращения по переменной х по Δх, тогда Δх стремится к 0.

Lim ΔxZ/Δх=dz/dx при Δх стремится к 0

Аналогично дается определение по переменной у

Lim ΔуZ/Δу=dz/dу при Δу стремится к 0

При нахождение частной производной по переменной х ,у=константа, а когда берем частную производную по переменой у то х=константа.

Определение Если функция z= f(x,y) дифференцируема в точке Р0(х0, у0), то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается

dz|p0=df(x0,y0)=f’x(x0,y0) Δx+f’y(x0,y0) Δy.

42.Дифференцирование сложной функции. Полная производная и полный дифференциал. Производная от функции заданной неявно. Скалярное поле. Производная по направлению и градиент. Касательная и нормальная плоскость к пространственной кривой. Касательная плоскость и нормаль к поверхности.

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке  .5. Частные производные и полный дифференциал 1-го порядка

Пусть даны функции, определённые в окрестностях на числовой прямой,   где   и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид: