1.Квадратные матрицы и их свойства. Определители и их свойства, вычесление определителей второго и третьего порядка. Минор и алгебраическое дополнение.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

 Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n.

Общие свойства:1)Общий множитель элемента одного столбца можно вынести за знак определителя;2)Велечина определителя не изменится,если к элементу1 столбца прибавить элементы 2 столбца умножив на произвольное одинаковое число.

Определители и их свойства

1. 

2. 

3. 

Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали.

Свойства:

1. Определитель не изменится, если его строки заменить столбцами, и наоборот.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю.

4. Общий множитель элементов можно вынести за знак определителя.

5. Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.

7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение.

Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю.

Определитель второго порядка вычисляется по формуле:

  

Определитель третьего порядка вычисляется по формуле:

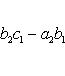
Минор

Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

Алгебраическим дополнением элемента   матрицы   называется число

,

где   — дополнительный минор, определитель матрицы, получающейся из исходной матрицы   путем вычёркивания i -й строки и j -го столбца.

2.Системы линейных алгебраических уравнений. Правило Крамера. Метод Гаусса.

 Системы линейных алгебраических уравнений -это система уравнений вида

Правило Крамера

Если в системе   линейных уравнений с   неизвестными   , то система имеет решение и притом единственное. Это решение задается формулами

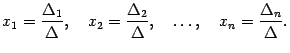
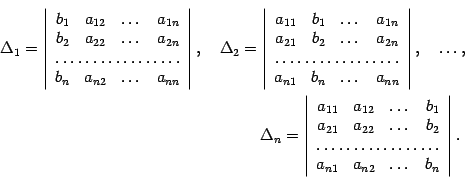
 Метод Гаусса

Определение. Две системы линейных уравнений называются равносильными, если множество всех их решений совпадает. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

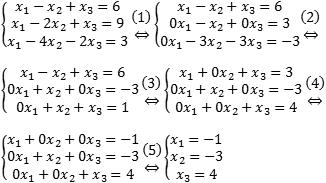
3.Матрицы любого порядка. Общие понятия. Виды матриц.Действия над матрицами(умножение на число, сложение и умножение матриц). Обратная матрица. Ранг матриц.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля , которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной.

Матрица, у которой всего одна строка  , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

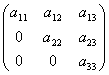
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей.

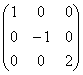
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. .

Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.

где

1. 

2. 

3. 

4. 

Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной, к данной.

1. 

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. 

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.

Обратная матрица.

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

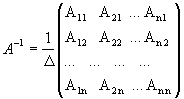
Обратная матрица матрице А, обозначается через А^1, так что В = А^1 и вычисляется по формуле, где А _{i j} - алгебраические дополнения элементов a _{i j} матрицы A.

Рангом матрицы   называется наибольший из порядков миноров матрицы   , отличных от нуля. Ранг нулевой матрицы считается равным нулю.