Угол между двумя прямыми!!!!

Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

20) Кривые второго порядка

 

Общий вид линии второго порядка:

  .                                                (1)

К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.

 

1. Окружность

Окружность – это множество точек плоскости, равноудаленных от данной точки (центра).

                                                          (2)

где  - радиус окружности,   и   - координаты центра окружности.

Если центр окружности совпадает с началом координат, то уравнение имеет вид

                                                                   (3)

Рис. 2

2. Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами).

Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках   и  :

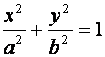                                                                            (4)

где   и   - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты   эллипса связаны соотношением 

Рис. 3

 

Если центр эллипса находится в точке  , то уравнение эллипса имеет вид:

                                                                  (5)

 

3. Гипербола

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Уравнение гиперболы с центром в начале координат и с фокусами в точках   и   имеет вид:

                                                                             (6)

где   - действительная полуось,

         - мнимая полуось.

 Коэффициенты   и   гиперболы связаны соотношением   .

       Прямые  - асимптоты гиперболы.

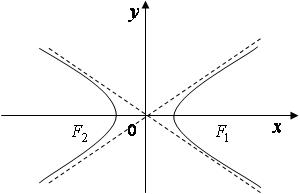
Рис. 4

 

Если центр гиперболы находится в точке  , то уравнение имеет вид:

                                                              (7)

4. Парабола

Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.

Уравнение параболы с вершиной в начале координат имеет вид:

                                                         ,                                                                                    (8)

где   - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .

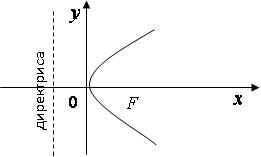
Рис. 5

 

Если вершина параболы находится в точке  , то уравнение имеет вид:

                                                                                                                    (9)

Задача 1.  Составить уравнение геометрического места точек, равноотстоящего от оси Оу и точки  .

Решение:  Возьмем на искомой линии произвольную точку  . Расстояние точки М от точки F определится по формуле расстояния между двумя точками:

Расстояние точки М до оси Оу определится:

Так как по условию  , то искомая кривая имеет уравнение:

        

Линия, определяемая полученным уравнением   является параболой.

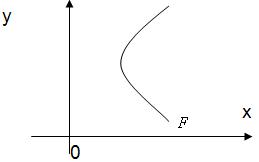
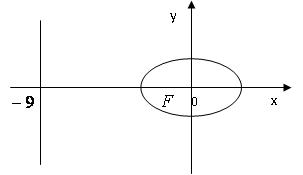
Задача 2.  Составить уравнение геометрического места точек, отношение  расстояний которых до точки F(-1; 0) и до прямой х = -9 равно 1/3.

Решение:  Возьмём на искомой кривой произвольную точку  .  Её расстояния от точки   и прямой составляют     

Из условия задачи следует:

Таким образом, искомая кривая имеет уравнение:

Приведём это уравнение к каноническому виду:

 - это уравнение эллипса с полуосями: