16)Определение смешанного произведения.
Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.
Определение.
Смешанным
произведением трех векторов 
и 
называется
действительное число, равное скалярному
произведению векторов 
и
,
где
-
векторное произведение векторов 
и 
.
Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.
Смешанное
произведение векторов
и
обычно
обозначают 
.
В таких обозначениях по определению
смешанного произведения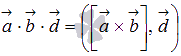 
17) Определение смешанного произведения.
Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.
Определение.
Смешанным произведением трех векторов и называется действительное число, равное скалярному произведению векторов и , где - векторное произведение векторов и .
Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.
Смешанное произведение векторов и обычно обозначают . В таких обозначениях по определению смешанного произведения .
Свойства смешанного произведения.
Из свойств векторного произведения и свойств скалярного произведения следуют следующиесвойства смешанного произведения:
;
;
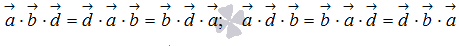Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.
Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.
Действительно,
если 
,
то по определению векторного произведения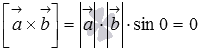 
,
следовательно, смешанное произведение
равно нулю, так как 
.
Если же
или 
,
то угол между векторами
и
равен 
,
следовательно, по определению скалярного
произведения векторов 
.
Свойства смешанного произведения обычно применяются при доказательстве тождеств или неравенств.
Рассмотрим несколько характерных задач.
Пример.
Докажите
равенство 
,
где 
-
некоторое действительное число.
Решение.
Преобразуем
левую часть равенства, обратившись к
третьему свойству смешанного
произведения:
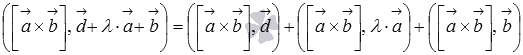
Выше
мы показали, что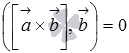 
,
следовательно,
По
первому свойству смешанного произведения 
,
а 
.
Таким образом, 
.
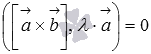Поэтому,
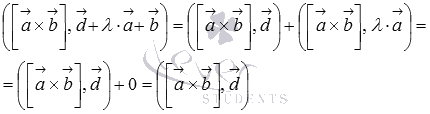
Что и требовалось доказать.
18) Декартовы прямоугольные координаты в пространстве
Декартова прямоугольна система координат в пространстве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в каком-либо порядке.
Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая координатная ось называется осью абсцисс, вторая - осью ординат, третья - осью апликат.
Начало координат обозначается буквой О, координатные оси - соответственно символами Ox, Oy, Oz.
Пусть
М - произвольная точка пространства, 
, 
, 
-
ее проекции на координатные оси (рис.
1).
Координатами
точки М в заданной системе называются
числа 
, 
, 
(рис.1),
где 
-
величина отрезка 
оси
абсцисс, 
-
величина отрезка
оси
ординат, 
-
величина отрезка 
оси
апликат. Число х называется абсциссой,
у - ординатой, z -
апликатой точки М. СимволM(x,
y, z)
обозначает, что точка М имеет координаты x,
y, z.
Плоскость Oyz разделяет все пространство на два полупространства; то из них, которое расположено в положительном направлении оси Ох, называется ближним, другое дальним. Плоскость Oxz также разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Оу, называется правым, другое - левым. Наконец, и плоскость Oxy разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Oz, называется верхним, другое - нижним.
Три плоскости Oxy, Oxz, Oyz вместе разделяют пространство на восемь частей; их называют координатными октантами и нумеруют так, как показано на рис. 2.