2.4.1 Примеры решения задач

Задача 1

На какую высоту над уровнем жидкости в сосуде поднимется жидкость в трубке пьезометра (рис. 2.3), если на поверхности жидкости гидростатическое давление р_о = 1,7 ат, плотность жидкости =1000 .

В системе СИ р_о = 1,7 ат = Па.

Жидкость в трубке пьезометра поднимается под действием избыточного давления р_изб = р_о – р_атм = 172264 – 101332 = 70932 Па.

Высота подъема жидкости

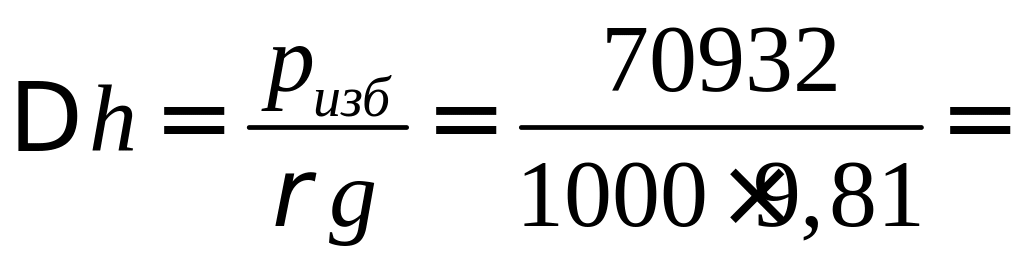7,23 м.

Задача 2

Для изоляции емкости, заполненной жидкостью с вредными газами, от атмосферного воздуха используют гидрозатворы. Гидрозатвор конструктивно представляет собой u – образную трубку – см. рис. 2.4. При технологическом выпуске части жидкости из емкости, в ней понизится давление, т.е. образуется вакуум р_вак = 2000 Па. Какая минимальная высота колена гидрозатвора обеспечит его нормальное функционирование? Какое абсолютное давление на дно сосуда возникнет при этом, если уровень оставшейся в сосуде жидкости Н = 2 м, а плотность ?

При возникшем вакууме р_вак = 2000 Па разность высот жидкости в коленах гидрозатвора составит 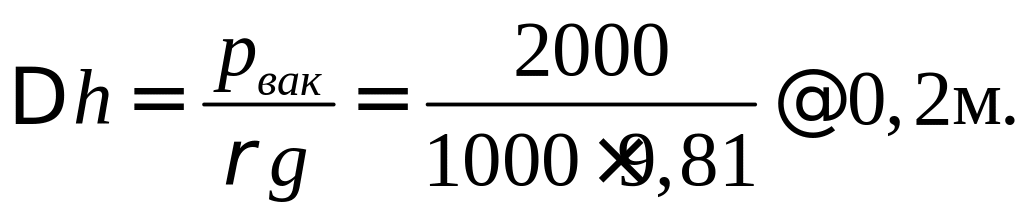Т.е. высота колена гидрозатвора должна быть не менее 0,2 м.

Давление на поверхности жидкости р_о = р_ат – р_вак = 101332 – 2000 = 99332 Па.

Давление на дно р_д = р_о + Па.

2.5 Эпюры гидростатического давления

Решение множества практических задач связано с построением эпюр давления. Эпюра давления – это график распределения давления по длине контура тела, погруженного в жидкость. Основное уравнение гидростатики (2.23) является уравнением прямой линии, где свободный член – это давление на поверхности жидкости - p₀, а угловой коэффициент – ρg. Изменение гидростатического давления по глубине, подчиняется линейному закону, поэтому для построения эпюры гидростатического давления действующего на плоскую фигуру необходимо найти только две точки, через которую проводится прямая линия.

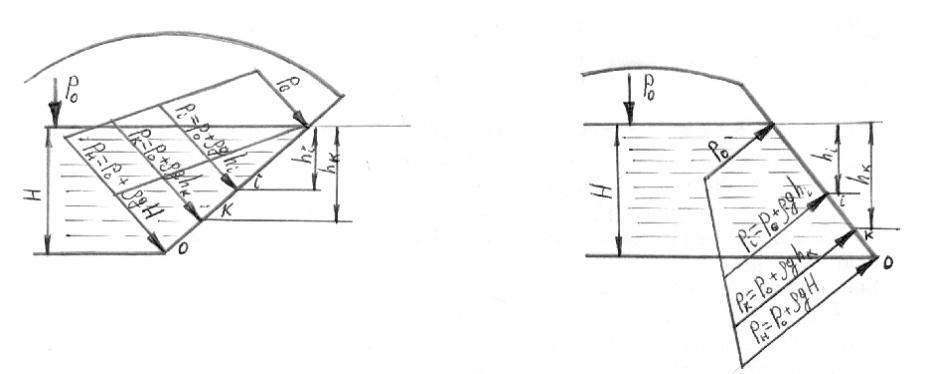
Рассмотрим построение эпюры избыточного давления, которое оказывает поток жидкости глубиной Н на плоскую стенку, имеющую произвольный угол наклона (рис. 2.5а и 2.5б).

Если на поверхности жидкости действует атмосферное давление, то задача упрощается, и нас интересует только избыточное давление, создаваемое самой жидкостью. Для построения эпюр выбираем две точки: первую – на пересечении поверхности жидкости со стенкой и вторую точку конца стенки в месте пересечения стенки с дном. В верхней точке жидкость избыточного давления не создаёт, потому что высота жидкости над этой точкой равна нулю. В нижней точке жидкость создаёт максимальное давление p_н=ρgH. Откладываем это значение на линии нормальной к стенке в любом выбранном нами масштабе. Вектор ρgH характеризует давление жидкости в точке О. Гидростатическое давление – величина векторная, т.к. кроме числового значения имеет направление действия. Направление давления всегда перпендикулярно поверхности, на которую оно действует. Эпюра имеет вид треугольника. Причём форма треугольника избыточного гидростатического давления зависит от величины плотности жидкости.

а) б)

Рис. 2.5. Схемы построения эпюр давления на произвольно наклонные прямые стенки

При наличии избыточного давления на поверхности жидкости (р₀>р_атм) эпюра принимает вид трапеции.

При этом промежуточное значение вектора давления в произвольной точке i определяемое длиной отрезка, равного р_i = p₀ + ρ g h_i , где h_i – глубина погружения точки i в жидкость.

1) p_н=p_o+ ρ g Н.

2) p_K=p_o+ ρ g h_K.

3 p_i = p_o + ρ g h_i.

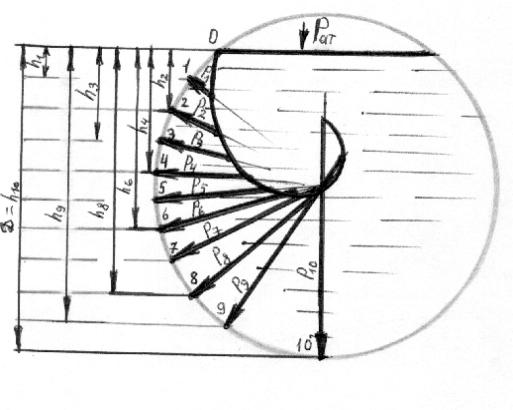
Рис.2.6. Схема построения эпюры давления на внутреннюю

цилиндрическую поверхность

Немного сложнее построение эпюры давления на криволинейную поверхность (рис.2.6). В связи с тем, что в каждой точке вектор гидростатического давления перпендикулярен поверхности, и величины векторов различны, эпюра приобретает сложную геометрическую криволинейную форму. Для построения такой эпюры двух точек совершенно недостаточно, и чем больше расчётных точек мы выберем на внутренней поверхности цистерны, тем точнее ломаная линия приблизится к плавной кривой.

Делим высоту уровня жидкости в цистерне на десять равных частей, и определим десять точек на внутренней поверхности цистерны, в которых мы будим откладывать рассчитанные значения векторов давления. Векторы давления в каждой расчётной точке направлены по нормали к поверхности, и следовательно, имеют радиальное направление, т.е. лежат на линиях, проходящих через центр. Величина каждого вектора находится как произведение: ρ g h_i, где h_i – высота столба жидкости над соответствующей расчётной точкой. В случае, если на поверхности жидкости давление р_изб, вектор давления удлиняется на это значение.