16.1.4. Многослойная цилиндрическая стенка

Рассмотрим передачу тепла через двухслойную цилиндрическую стенку (рис. 16.4) при установившемся тепловом потоке. Температуры горячей и холодной сред t_ж1 и t_ж2, соответственно.

Известны диаметры обоих слоев d₁, d₂ и d₃. Коэффициенты теплопроводности слоев постоянны и равны ₁ и ₂, коэффициенты теплоотдачи со стороны горячей и холодной сред _ и _. Неизвестны температуры поверхностей, контактирующих с горячей и холодной средами t_с1 и t_с3, а также температура соприкосновения цилиндрических слоев t_с2.

Так как тепловой поток стационарный, то от горячего теплоносителя к поверхности к единице длины трубы пойдет тепловой поток

.

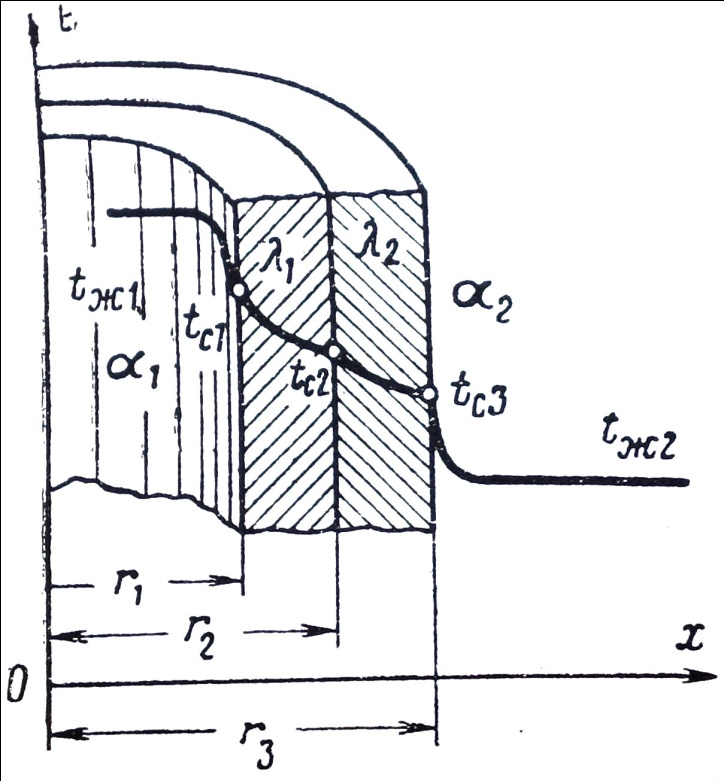
Рис. 16.4. Теплопередача через многослойную цилиндрическую стенку

Этот же тепловой поток пройдет через внутреннюю трубу

и через наружную трубу

,

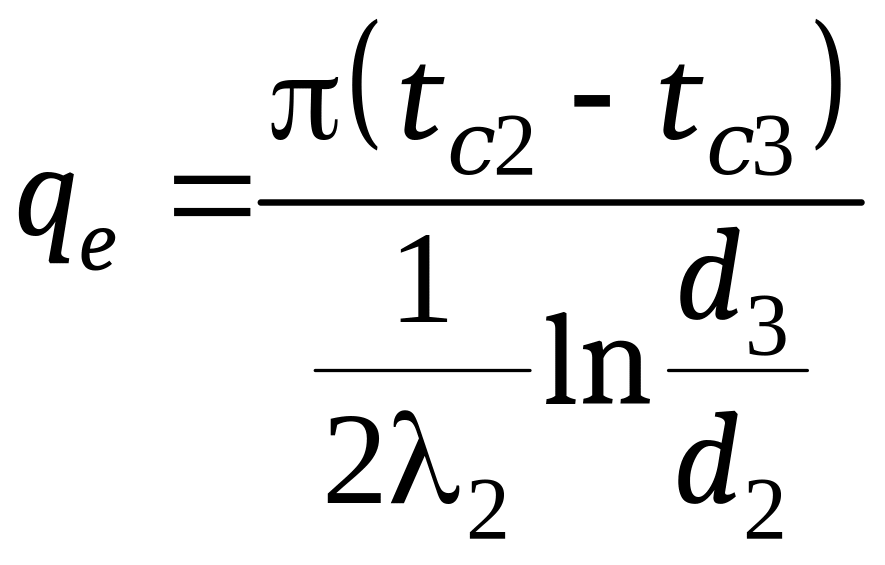и, наконец, от наружной поверхности внешней трубы будет воспринят холодным теплоносителем

.

Из этих уравнений определяем частные температурные напоры:

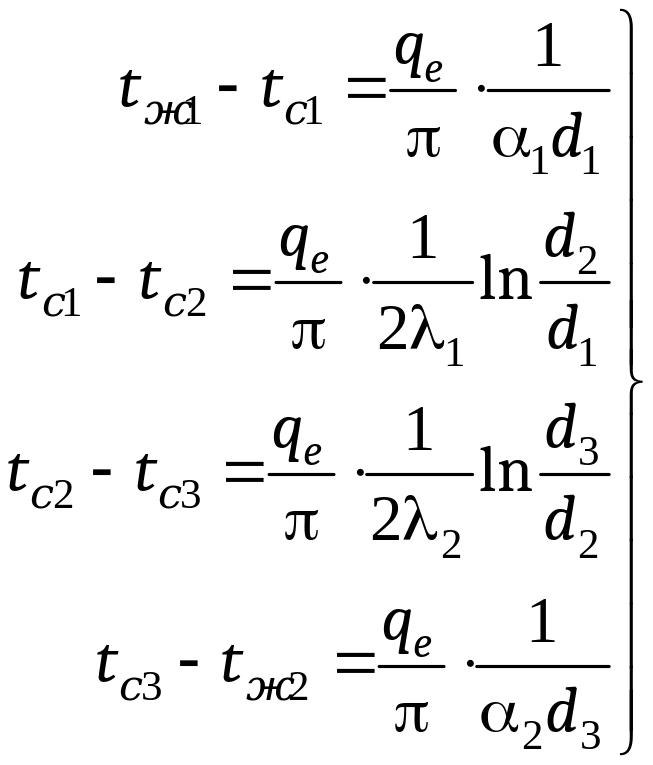(16.14)

Складывая отдельно левые и правые части уравнений системы, получим значение полного температурного напора

.

Отсюда значение линейного теплового потока

; (16.15)

. (16.16)

Здесь — полное линейное термическое сопротивление теплопередачи двухслойной цилиндрической поверхности;

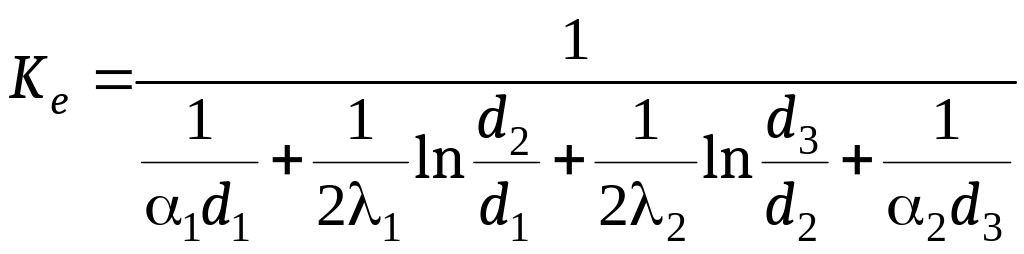— линейный коэффициент теплопередачи.

Для многослойной стенки значение линейного коэффициента теплопередачи будет иметь вид

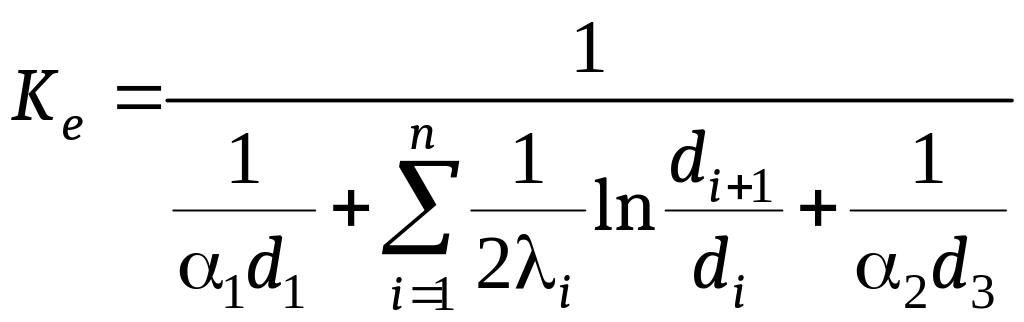. (16.17)

Значение неизвестных температур стенок t_с1, t_с2 и t_с3 можно найти из уравнений частных температурных напоров

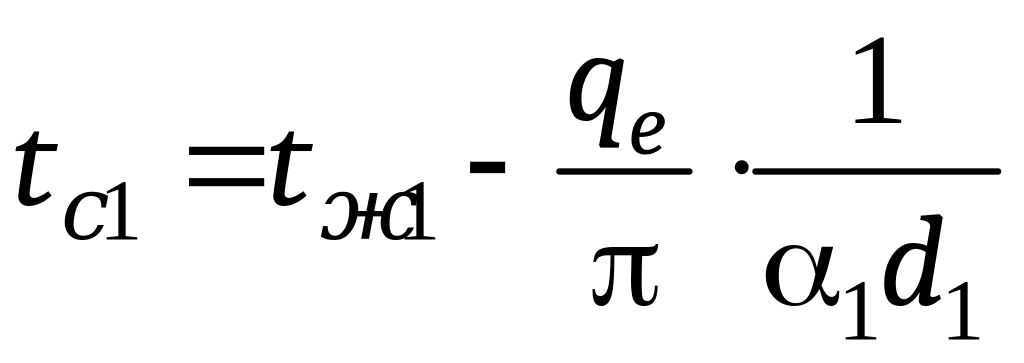; (16.18)

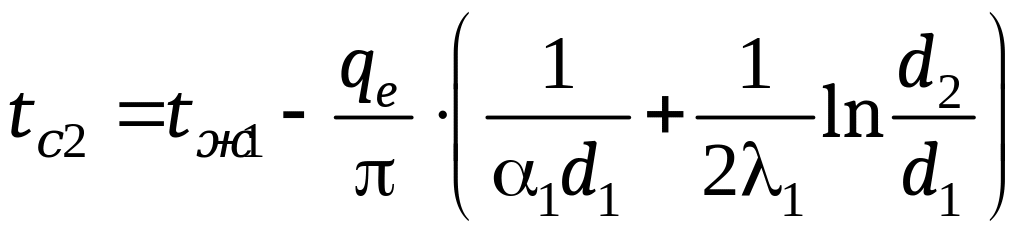; (16.19)

; (16.20)

16.1.5. Упрощение расчетных формул

Так как формулы теплопередачи для труб довольно громоздки, при этом иногда вызывает затруднения определения величин натуральных логарифмов, то при проведении практических расчётов применяют некоторые упрощения. Вместо формул для определения линейного теплового потока для однослойной трубы (6.10) применяется формула для плоской поверхности, которая в применении к трубе длиной 1 м примет вид

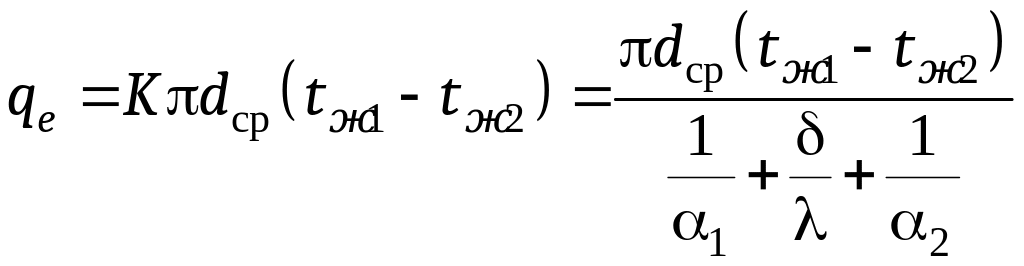. (16.21)

Здесь K — коэффициент теплопередачи плоской стенки;

d_ср — средний диаметр стенки, ;

 — толщина стенки трубы .

Для многослойной стенки формула приобретет вид

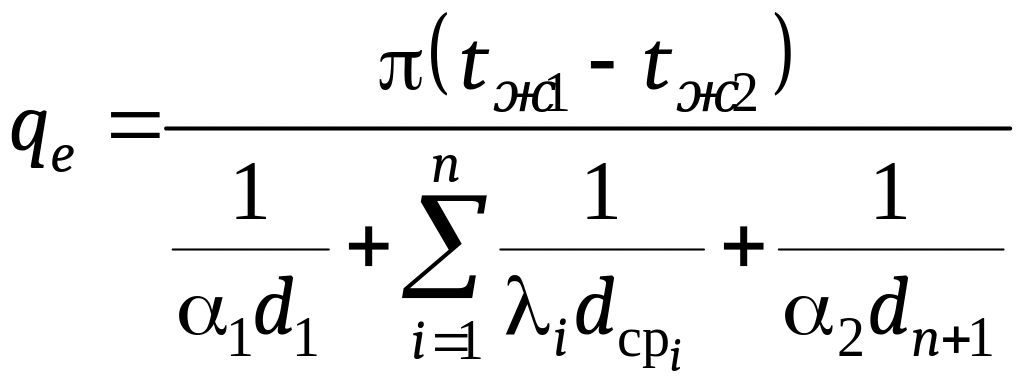. (16.22)

где — средний диаметр i-того слоя;

_i — теплопроводность i-того слоя.

Погрешность при проведении расчетов не превышает 3-4 %, если 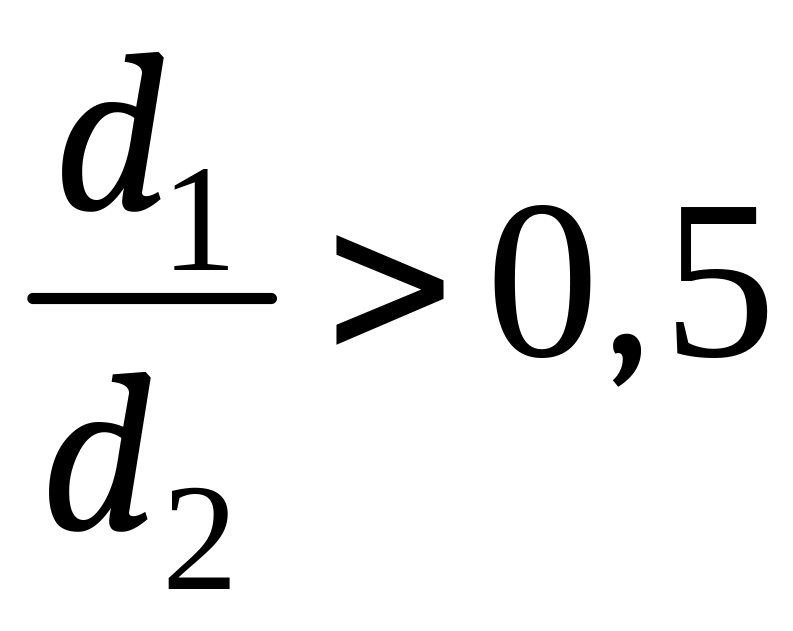. К тому же, погрешность можно существенно снизить, если при выборе d_ср соблюдать следующие правила:

1. В случае ₁ >> ₂ следует принять d_ср = d₂.

2. При ₁ ≈₂, то .

3. В случае, если ₁ << ₂ , то d_ср = d₁

То есть, при расчете теплопередачи по формуле (16.21) вместо d_ср принимается тот диаметр, со стороны которого теплоотдача минимальна.

При проведении расчетов для их упрощения следует пренебрегать относительно малыми термическими сопротивлениями.

16.1.6. Примеры решения задач

Задача 1. В процессе эксплуатации трубки парового газотрубного котла покрылись слоем сажи _с = 1 мм и накипи _н = 2 мм. Температура греющих газов t_г = 1000° C, температура кипящей воды t_х = 200° C.

Коэффициенты теплоотдачи со стороны газов _г = 150 Вт/(м²·К), со стороны кипящей воды _х = 7000 Вт/(м²·К). Определить уменьшение плотности теплового потока в результате загрязнений, если трубки котла, сажа и накипь имеют следующие параметры: d₁ = 32 мм, d₂ = 40 мм, _ст = 50 Вт/(м²·К), _с = 1 мм, _с = 0,08 Вт/(м²·К), _н = 2 мм, _н = 0,8 Вт/(м²·К).

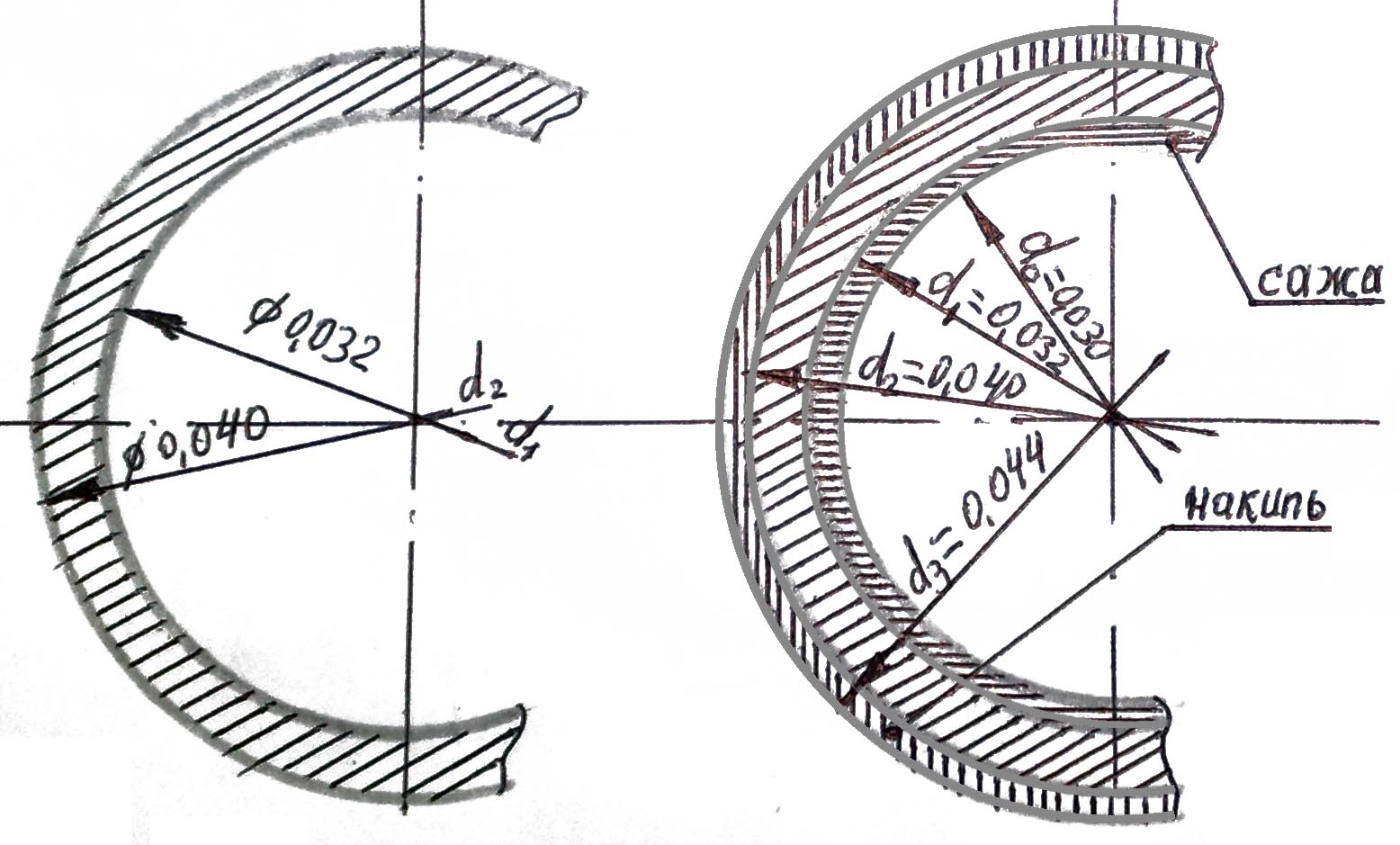
Рис. 16.5 Трубка газотрубного котла: слева чистая труба, справа — труба с загрязнениями

Плотность теплового потока через чистые трубы

.

Температура греющих газов зависит только от количества и качества сжигаемого топлива, температура кипения воды зависит только от давления. Обе эти температуры не зависят от количества и качества загрязнений. Поэтому плотность линейного теплового потока через загрязненную поверхность

.

То есть, для уменьшения плотности теплового потока необходимо рассчитать значения линейных коэффициентов теплопередачи для чистой и загрязненной труб.

.

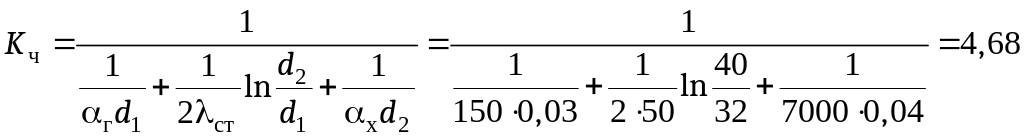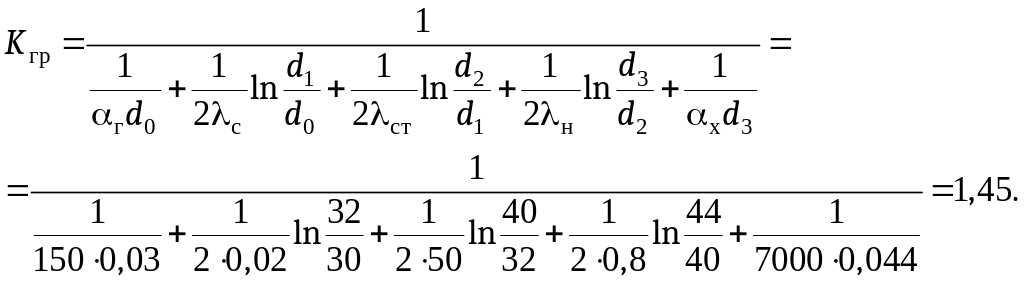
Здесь

d₀ = d₁ – 2_с = 0,032 – 2·0,001 = 0,030 м;

d₃ = d₂ – 2_н = 0,040 + 2·0,002 = 0,044 м,

где d₀ — внутренний диаметр трубы со слоем сажи. Это та поверхность, с которой будут контактировать греющие газы.

d₃ — наружный диаметр слой накипи, с которым будет контактировать кипящая вода.

Мы видим, что даже такие незначительные толщины загрязнений приводят к уменьшению плотности теплового потока более чем в три раза.

.

Задача 2. Определить площадь поверхности нагрева водо-водяного подогревателя, выполненного из латунных труб 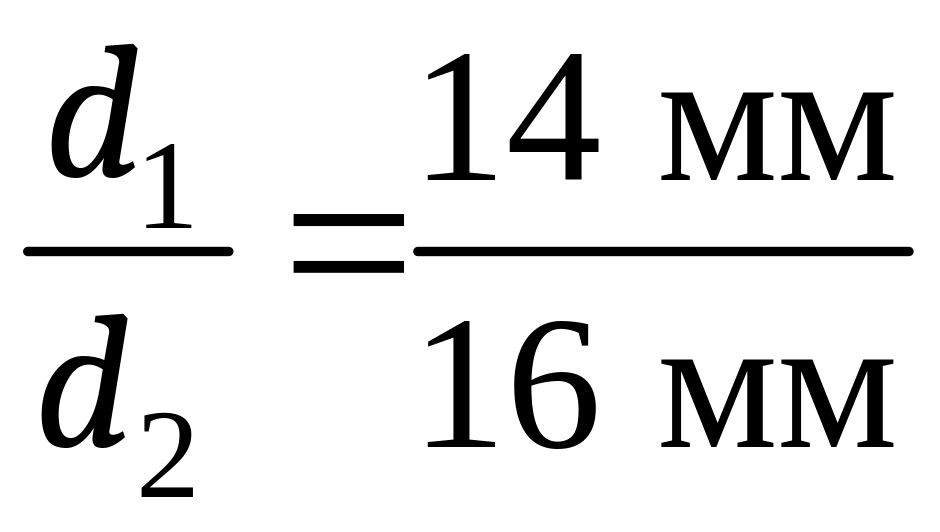теплопроводность которых _л = 120 Вт/(м²·К). Коэффициент теплоотдачи со стороны горячей воды _г = 5000 Вт/(м²·К), со стороны холодной воды _х = 3000 Вт/(м²·К), средние температуры — горячей воды t_г = 95° C, холодной воды — t_х = 50° C, тепловая мощность нагревателя Q = 300 Вт.

Тепловая мощность нагревателя

Здесь K_Fх — коэффициент теплопередачи, отнесенный к наружному диаметру труб;

F_х — площадь наружной поверхности труб, м².

Коэффициент теплопередачи, отнесенный к наружной поверхности (6.8), омываемой холодной водой,

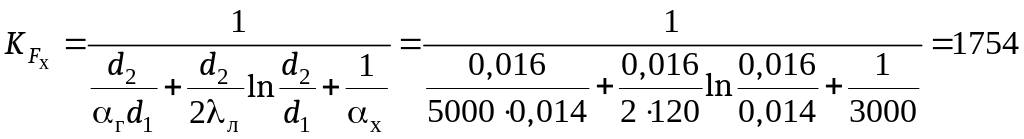Вт/(м²·К).

Необходимая площадь теплообменной поверхности

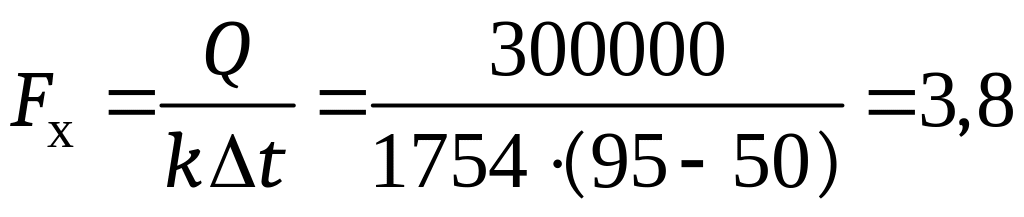м².

Необходимая длина труб, составляющих поверхность теплообмена, F_х = d₂l. Отсюда

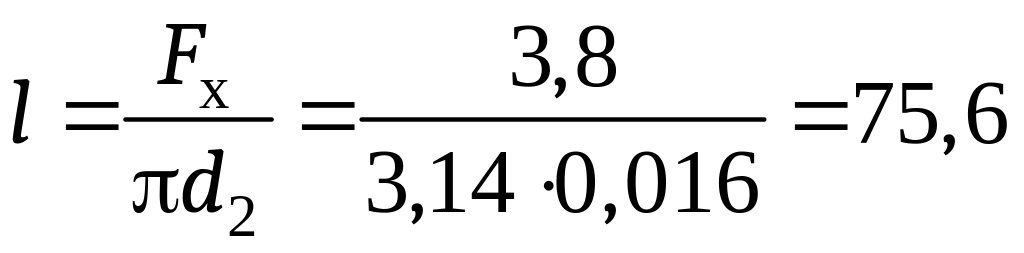м.

Задача 3. Паропровод наружным и внутренним диаметрами 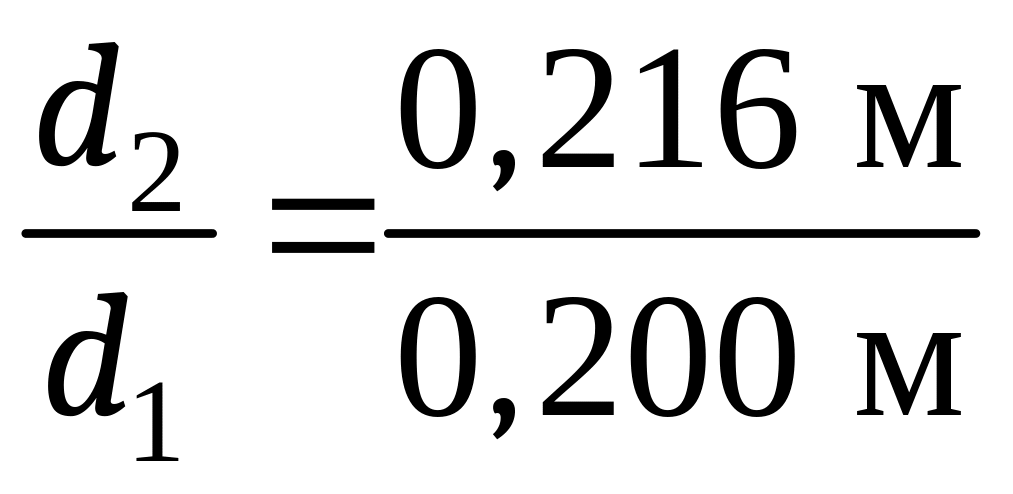покрыт слоем изоляции _из = 120 мм, теплопроводность которой _из = 0,1 Вт/(м²·К). Температура пара t_г = 30° C, температура наружного воздуха t_х = 25° C. Теплопроводность стали  = 40 Вт/(м²·К), коэффициенты теплоотдачи: со стороны пара _г = 100 Вт/(м²·К), со стороны воздуха _х = 8 Вт/(м²·К). Определить линейную плотность теплового потока и температуру на поверхности изоляции.

.

.

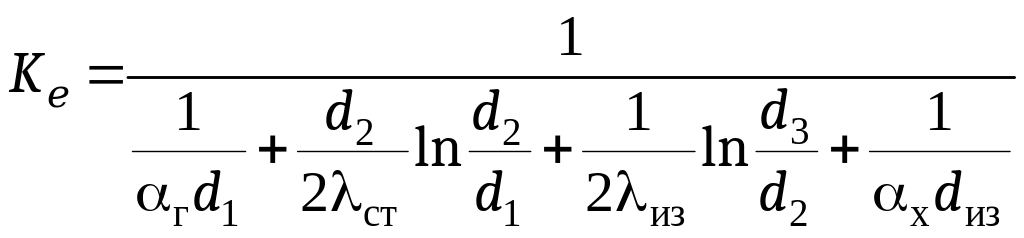где d_из = d₂ + _из = 0,216 +0,120·2 = 0,456 м.

.

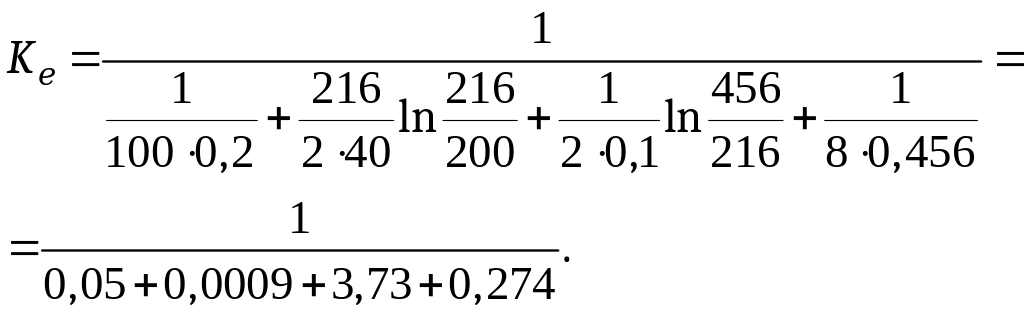Так как первые два термических сопротивления исчезающе малы по сравнению с остальным, в расчетах ими пренебрегаем.

Вт/(м²·К).

Тогда

Вт/м.

Температура поверхности изоляции

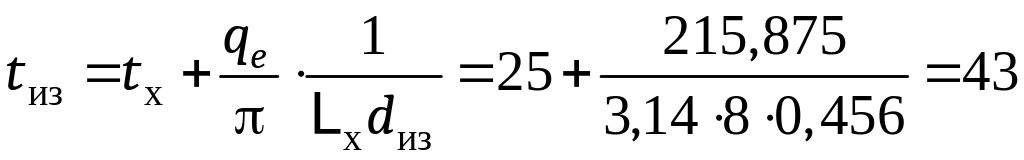° C.