2.2 Дифференциальные уравнения равновесия жидкости

Рассмотрим жидкость, находящуюся в равновесии. Выбираем систему произвольных координат с центром в точке O и зафиксируем произвольную точку A с координатами x, y, z (см. рис. 2.1).

Построим вокруг этой точки элементарный параллелепипед с гранями равными: dx, dy, dz. На выделенный объём действуют внешние силы, поэтому он будет находиться в равновесии, если сумма проекций всех действующих сил на каждую ось будет равна нулю. Определим все внешние силы — массовые и гидростатического давления — действующие на грани параллелепипеда со стороны окружающей жидкости. Обозначим проекции массовых сил, отнесенных к единице массы, на координатные оси: А_x, A_y, A_z. Тогда проекции массовых сил на ось х

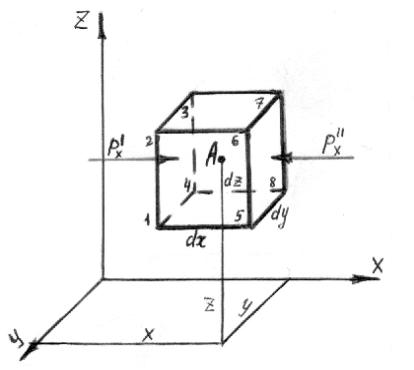
Рис. 2.1. Элементарный параллелепипед, описанный вокруг точки А.

dF_x = A_xdm = A_xρdxdydz, (2.1)

здесь dm — масса элементарного объёма жидкости

dm = ρdV = ρdxdydz. (2.2)

Аналогично, проекции массовых сил на оси y и z:

dF_y = A_ydm = A_yρdxdydz; (2.3)

dF_z = A_xdm = A_zρdxdydz. (2.4)

Теперь рассмотрим силы гидростатического давления, действующие на параллельные грани параллелепипеда 1–2–3–4 и 5–6–7–8. Обозначим силы давления буквами и . В соответствии с первым свойством гидростатического давления силы давления действуют нормально к поверхностям 1–2–3–4 и 5–6–7–8 и являются силами сжимающими. Если в точке А гидростатическое давление р, то на расстоянии , на плоскостях 1–2–3–4 и 5–6–7–8 будут действовать давления

(2.5)

. (2.6)

где p/ x – градиент давления на расстояние от точки А.

Тогда проекции сил действующие на площади dy^.dz поверхностей 1–2–3–4 и 5–6–7–8:

, (2.7)

. (2.8)

Уравнение равновесия параллелепипеда относительно оси Х получим, приравняв к нулю сумму проекций на ось Х всех внешних сил

. (2.9)

Подставив в уравнение (2.9) значения всех действующих сил получим

. (2.10)

Раскроем скобки

. (2.11)

Проведя сокращения и перегруппируя члены уравнения, получим

. (2.12)

Аналогично получаем уравнения равновесия относительно осей у и z

. (2.13)

(2.14)

Таким образом, скомпонована система уравнений (2.12, 2.13, 2.14) равновесия жидкости, которую впервые получил Л.Эйлер

(2.15)

2.3 Основное уравнение гидростатики

Преобразуем систему уравнений (2.15). Для этого умножим первое уравнение на dx, второе – на dy, третье – на dz

. (2.16)

Сложив левые и правые части уравнения системы, получим дифференциальное уравнение равновесия жидкости

. (2.17)

Правая часть уравнения представляет собой полный дифференциал давления , тогда можно записать вместо (2.17)

. (2.18)

Полученное уравнение является основным уравнением гидростатики в дифференциальной форме. Однако, гораздо чаще пользуются уравнением в более простой форме, когда из объёмных сил действует только сила тяжести. В этом случае A_x=0, A_y=0, A_z= - g и уравнение запишется в виде

. (2.19)

Проинтегрировав (2.19), получим основное уравнение гидростатики в виде

. (2.20)

Проиллюстрируем полученное уравнение. Для этого рассмотрим замкнутый сосуд с жидкостью, плотность которой и на поверхности которой давление р_о

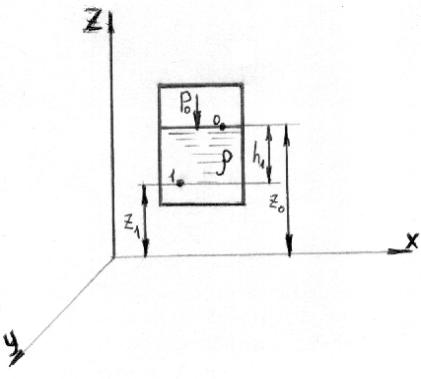
Рис. 2.2. Замкнутый сосуд с жидкостью

Выбираем произвольную точку 1, расположенную на высоте z₁. На основании основного уравнения гидростатики (2.20) можно записать

(2.21)

здесь p₁ - гидростатическое давление в точке 1;

z₁ - высота положения выбранной точки над плоскостью сравнения.

Сумма гидростатического давления и произведения ρgz является величиной, постоянной для данного сосуда. Если для сравнения выберем точку 0 на поверхности жидкости, высота которой z₀ , то уравнение (2.21) приобретёт вид

откуда,

(2.22)

где (z₀- z₁)= h₁ глубина погружения точки 1.

Соответственно, давление в произвольной точке будет равно сумме давления на поверхности жидкости плюс давление столба жидкости над этой точкой

(2.23)

Полученное уравнение (2.23) – это ещё одна, часто употребляемая формула основного уравнения гидростатики.