12.5. Теплопроводность плоской стенки

12.5.1. Однослойная стенка

Рис. 12.1Однородная плоская стенка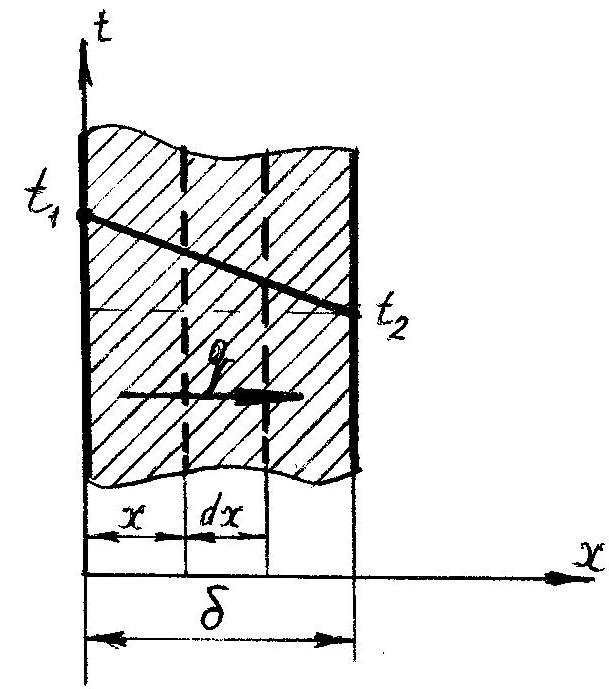

Рассмотрим плоскую стенку толщиной , изготовленную из однородного материала (рис. 12.1), коэффициент теплопроводности которого постоянен и равен . На наружных поверхностях стенки поддерживаются постоянные температуры t₁ и t₂.

Изменение температуры происходит только в направлении оси Х. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси Х. Выделим внутри стенки на расстоянии х от левого края слой толщиной dx (см. рис. 12.1) Этот слой будет ограничиваться двумя плоскостями, изображенными пунктирными линиями, поверхности которых будут изотермичны. Рассматривая стационарный процесс теплопроводности (q = const), на основании закона Фурье можно записать

.

Разделим переменные и проинтегрируем полученное выражение

, (12.7)

, (12.8)

Постоянную интегрирования C можно определить из граничных условий:

при X = 0	t = t1 = C
при X = 	t = t2

_{Подставляя эти значения в уравнение (12.8), получим}

. (12.9)

Отсюда

, Вт/м². (12.10)

Следовательно, количество тепла, передаваемое через один квадратный метр площади стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности  и разности температур наружных поверхностей и обратно пропорционально толщине стенки . Уравнение (12.10) является расчётной формулой теплопроводности плоской стенки. Оно связывает между собой четыре величины — удельный тепловой поток q, теплопроводность , толщину стенки  и разность температур. Зная значения любых трех величин (или задаваясь), можно определить четвертую. Необходимо запомнить, что отношение называют тепловой проводимостью стенки, а обратную величину — термическим (или тепловым) сопротивлением теплопроводности.

Если в уравнение (12.8) подставить найденные значения и , то можно получить уравнение температурной кривой

. (12.11)

Принимая значение теплопроводности постоянным, получаем изменение температуры по линейному закону. В действительности, из-за того что теплопроводность является функцией температуры, формула температурной кривой будет сложнее. Для строительных и изоляционных материалов и поэтому

. (12.12)

Разделив переменные, проинтегрировав и найдя из граничных условий константу интегрирования, можно получить уравнение температурной кривой с учетом меняющейся в различных температурных зонах теплопроводности.

12.5.2. Многослойная стенка

В производственной практике однослойных стенок практически нет. Даже однослойная поверхность водогрейной трубы в котле с одной стороны покрыта сажей, с другой — накипью. Любая технологическая, строительная или отопительная конструкция имеет несколько слоев — загрязнения, масло, накипь, краска, штукатурка... Многослойными называются стенки, состоящие из нескольких разных, но однородных слоев.

Рассмотрим трехслойную стенку (рис. 12.2), состоящую из трех плотно прилегающих друг к другу слоёв с толщинами ₁, ₂, ₃. Каждый слой характеризуется своей постоянной теплопроводностью ₁, ₂ и ₃ соответственно. Известны также температуры наружных поверхностей t₁ и t₄. Тепловой контакт между слоями — идеальный, без зазоров и соответственно без воздушных прослоек, температуры в местах контакта слоев обозначаем t₂ и t₃.

Рис. 12.2. Трёхслойная цилиндрическая стенка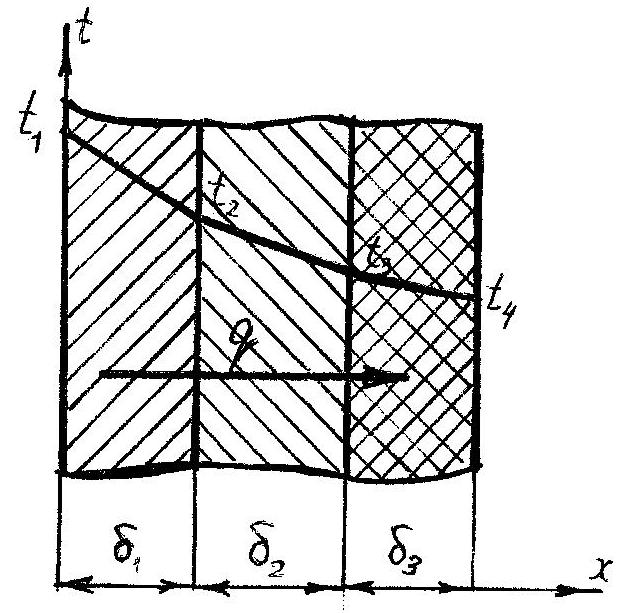

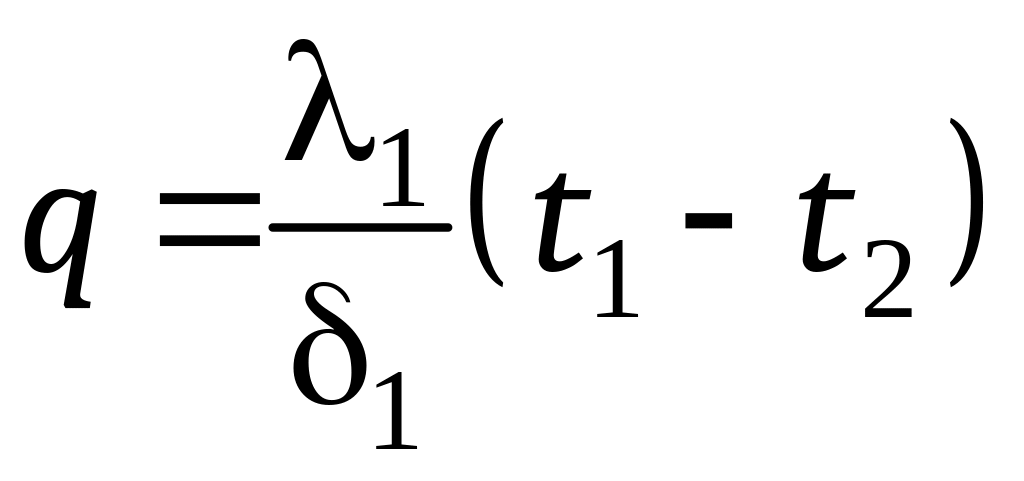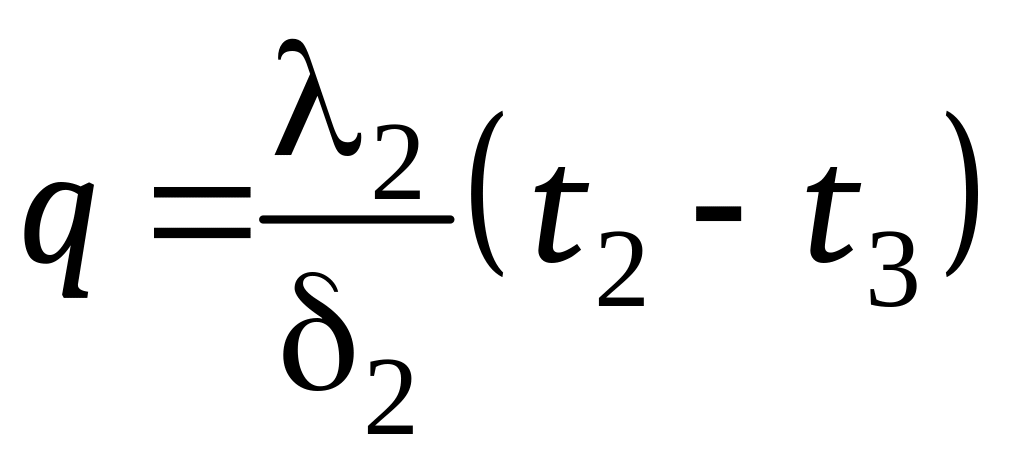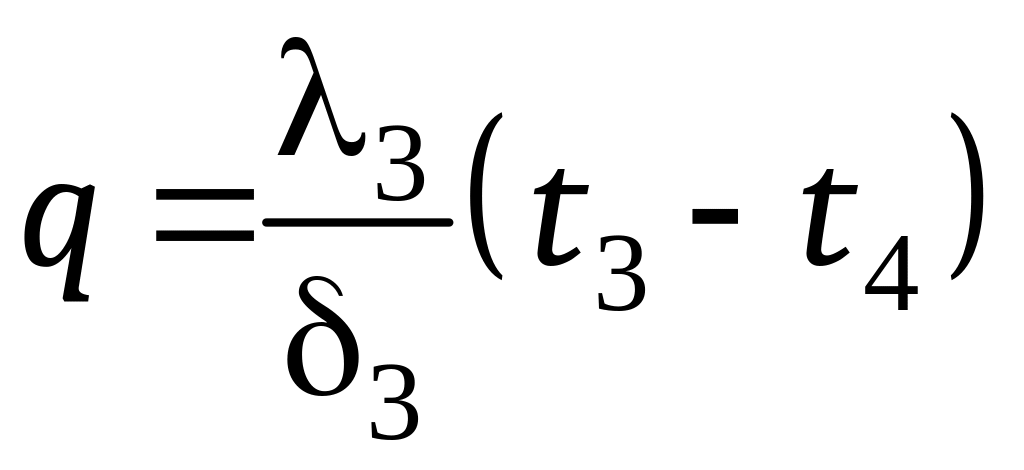Так как температуры наружных поверхностей постоянны, тепловой поток — установившийся, и соответственно, количество теплоты проходящее в единицу времени — неизменно. При стационарном режиме удельный тепловой поток q постоянен и для всех слоев одинаков. Поэтому можно записать для каждого из слоев:

;

;

.

Из приведенных выражений легко определить значения локальных разностей температур на границах каждого слоя:

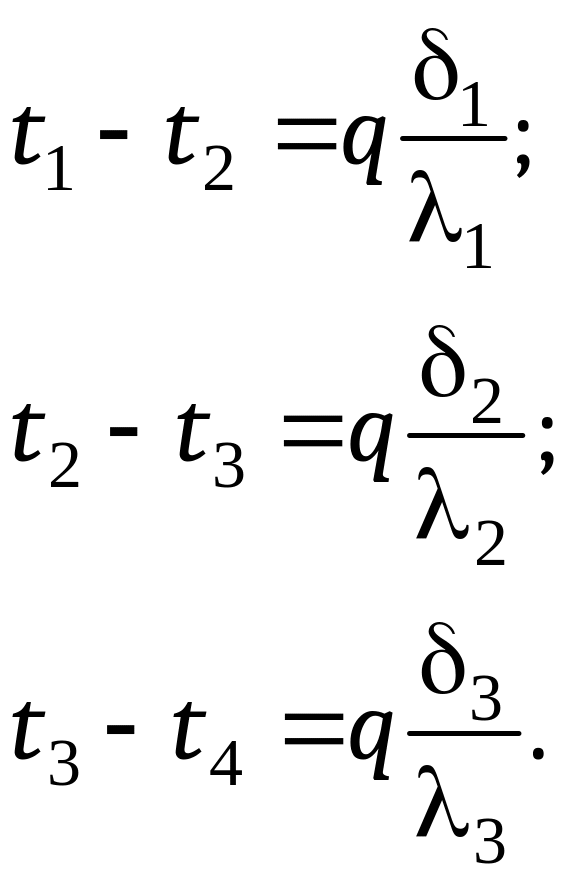(12.13)

Складывая почленно левые и правые части уравнений получим

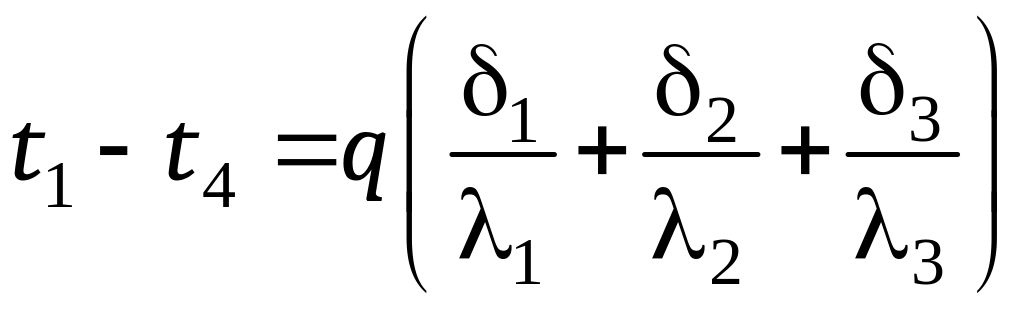. (12.14)

Откуда

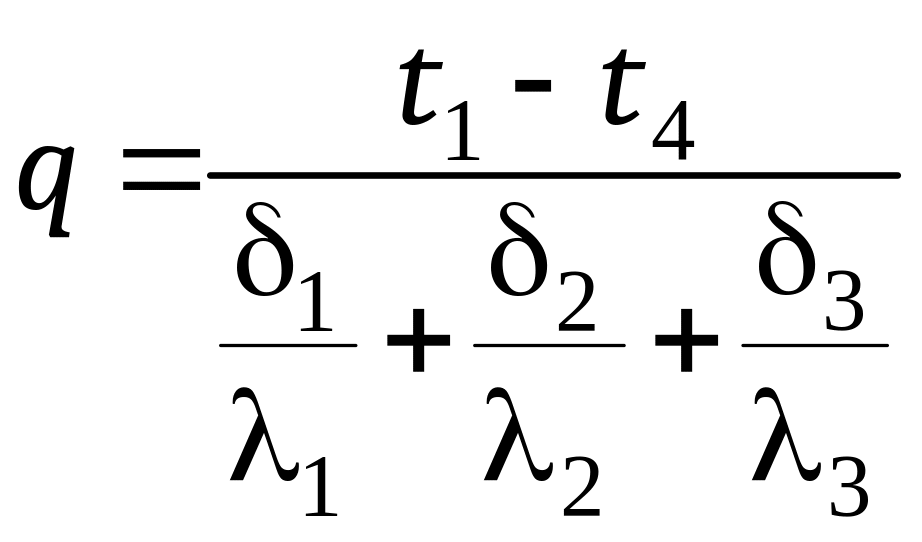. (12.15)

Уравнение (12.15) — расчетная формула теплопроводности трехслойной стенки. По аналогии, для стенки, имеющей n слоев, можно записать

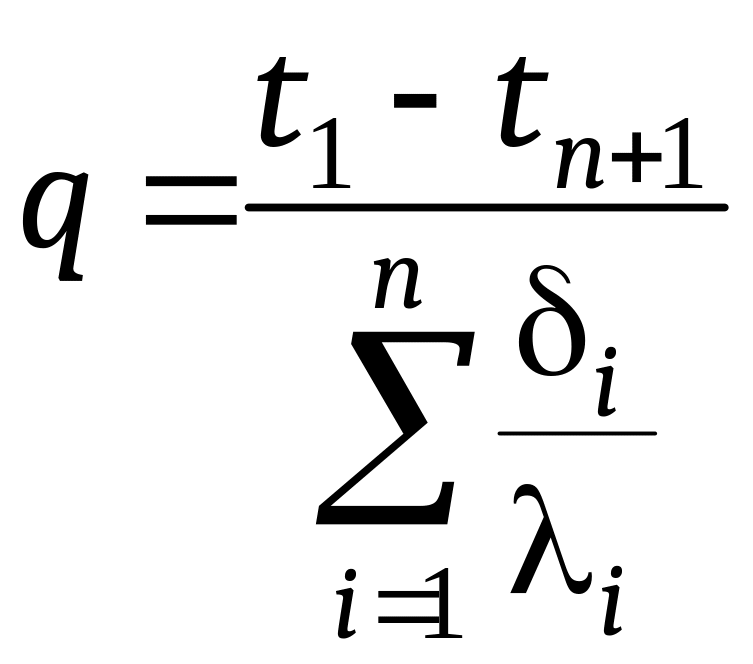. (12.16)

Здесь t₁ и t_n+1 — температуры на наружных поверхностях n-слойной стенки;

— общее термическое сопротивление многослойной стенки, равное сумме частных термических сопротивлений всех слоев.

При условии, что коэффициент теплопроводности каждого слоя — величина постоянная, температура внутри каждого слоя изменяется по прямой, но в целом, для многослойной стенки она — ломаная линия.

Температуры на стыке слоев t₂ и t₃ можно определить из системы уравнений (12.13)

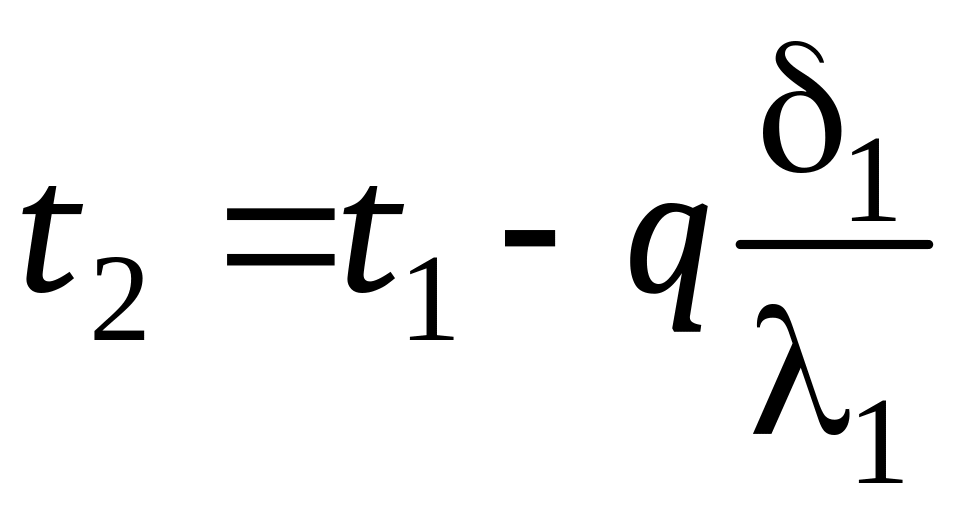, (12.17)

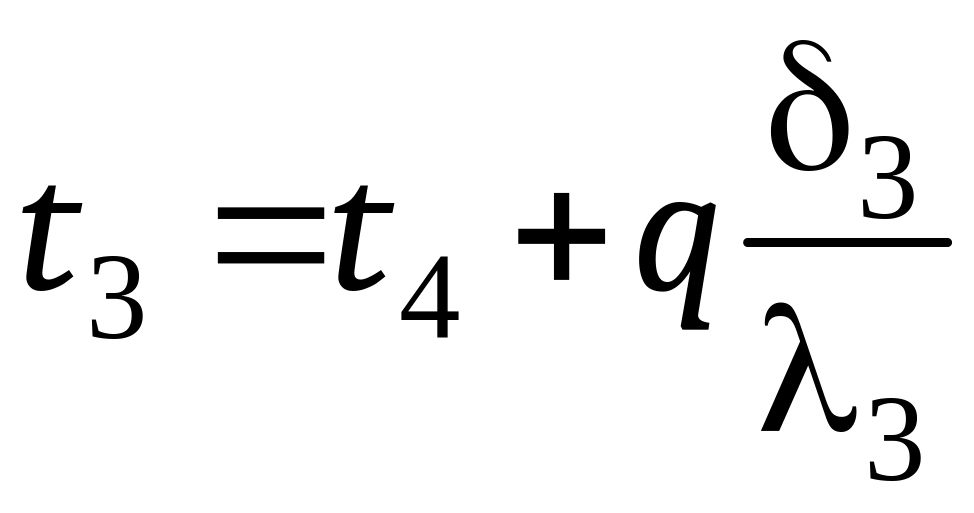. (12.18)

Иногда многослойную стенку рассчитывают как однослойную толщиной  = ₁ + ₂ + ₃. При этом, в расчет вводится эквивалентный коэффициент теплопроводности _эк, который определяется из условия:

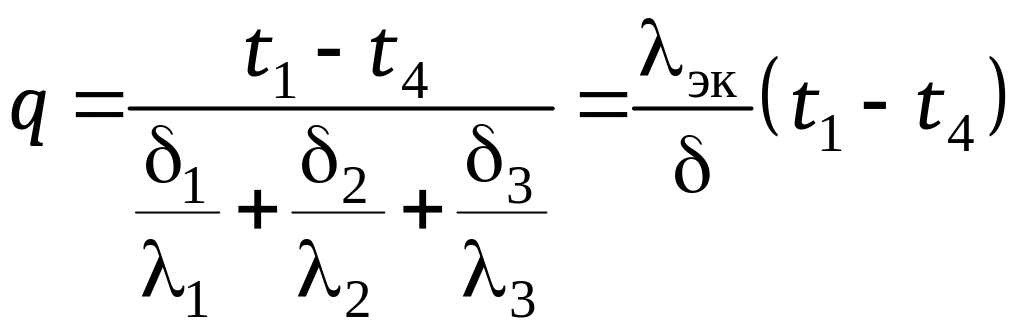, (12.19)

отсюда

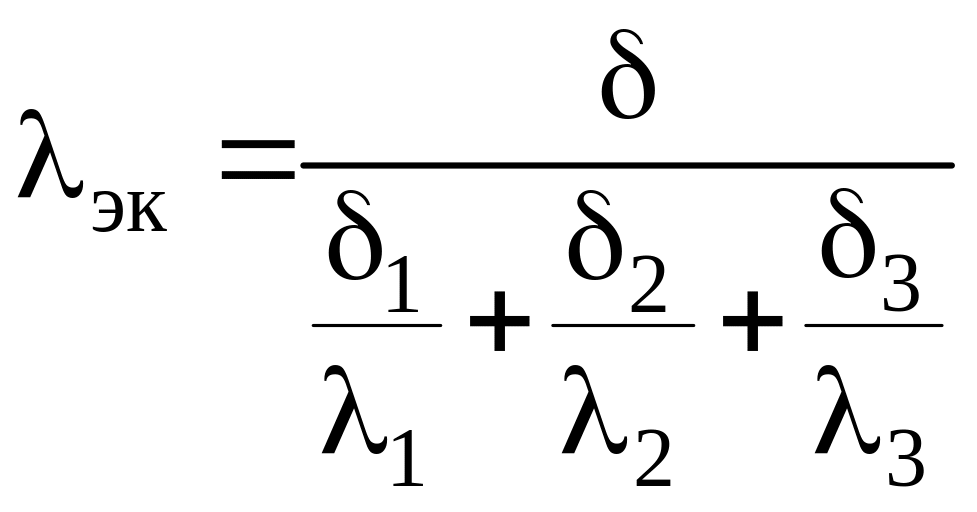. (12.20)

При выводе расчетной формулы для многослойной стенки (12.16) предполагалась, что слои плотно прилегают друг к другу и благодаря идеальному тепловому контакту соприкасающиеся поверхности имеют одинаковую температуру. При шероховатой поверхности между слоями возникают воздушные зазоры. А так как теплопроводность воздуха в нормальных условиях  = 0,025 Вт/(м·К), то наличие даже очень тонких воздушных прослоек резко ухудшает теплопроводность конструкции.