7.1.2. Расчеты термодинамических процессов

Рассмотрим частные случаи термодинамических процессов.

Изохорный процесс ( ).

Изохорным называется термодинамический процесс, протекающий при постоянном объеме (изос – равный, хора – пространство, греч.). Примером изохорного процесса может служить нагревание или охлаждение газа в закрытом сосуде (в баллоне). На практике этот процесс встречается в циклах ДВС при сжатии топлива.

Уравнение изохорного процесса получаем из уравнений состояния идеального газа и в начальной и конечной точках процесса. Отсюда

(7.1)

Давление в изохорном процессе пропорционально температуре газа.

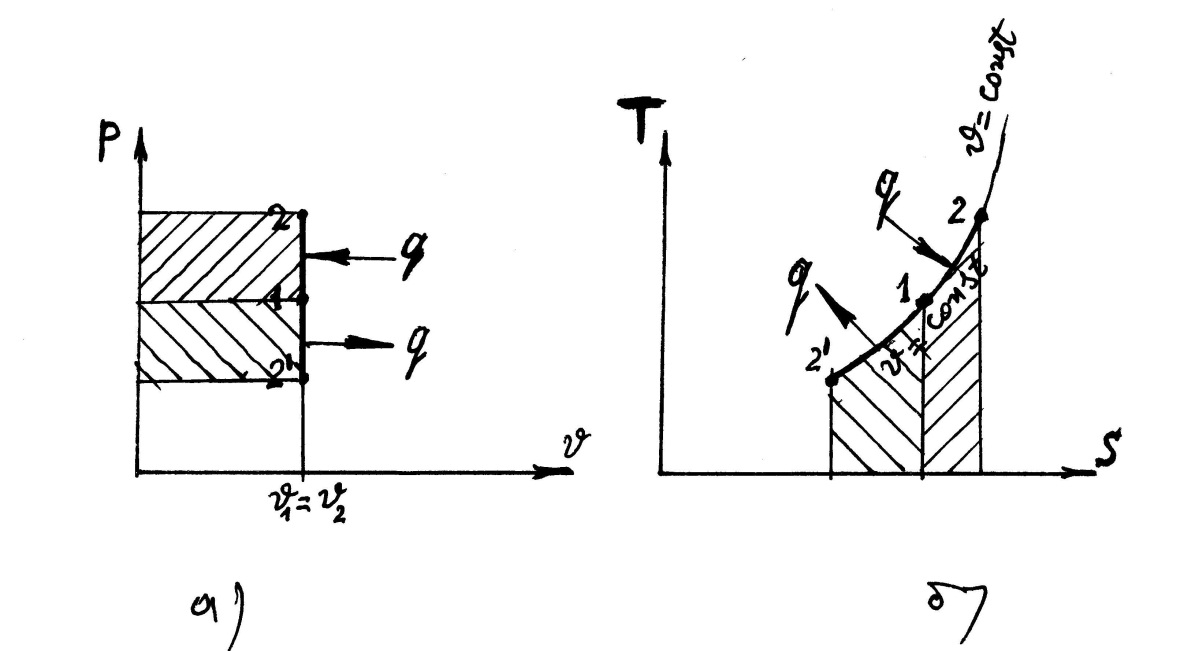
Рис. 7.1 а) рабочая диаграмма изохорного процесса; б) тепловая диаграмма изохорного процесса.

На рисунке 7.1 показаны процессы подвода и отвода теплоты при в и диаграммах. Процесс 1-2 это процесс подвода теплоты, процесс 1-2' – отвод теплоты. Работа в изохорном процессе равна нулю, так как и . Все подведенное (или отведенное) количество теплоты идет на изменение внутренней энергии.

Следовательно, доля тепла пошедшего на увеличение внутренней энергии

(7.2)

Количество теплоты определяется через изохорную теплоемкость и разность температур

, Дж/кг (7.3)

Это количество теплоты можно определить также как площадь под кривой процесса в тепловой диаграмме.

Изобарный процесс.

Термодинамический процесс, протекающий при постоянном давлении называется изобарным (изос – равный, барос – тяжесть, греч.).

Из уравнений состояния

получаем соотношение

(7.4)

Отношение удельных объемов в изобарном процессе пропорционально отношению абсолютных температур.

Этот процесс, являющийся составной частью циклов ДВС и ГТУ изображен на рис. 7.2. В процессе 1-2 осуществляется подвод, а в процессе 1-2' – отвод теплоты.

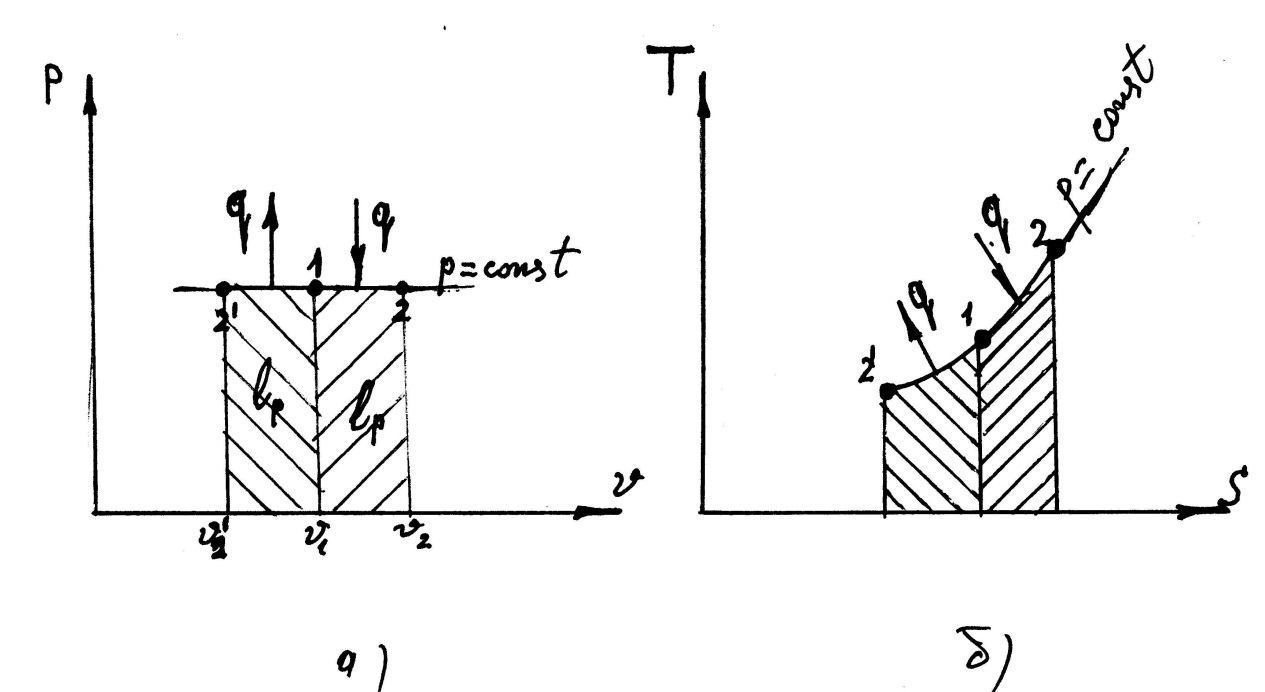
Рис 7.2 а) рабочая диаграмма изобарного процесса; б) тепловая диаграмма изобарного процесса.

На рис. 7.2(а) площадь под кривой процесса 1-2 соответствует количеству полученной работы, площадь под процессом 1-2' – соответствует количеству работы затраченной.

Изменение внутренней энергии в процессе 1-2

(7.5)

Полученная работа в процессе 1-2

(7.6)

Затраченная в процессе 1-2' теплота

(7.7)

Доля теплоты затраченной на изменение внутренней энергии

Следовательно, на производство работы израсходовано всего .

Изотермический процесс.

Термодинамический процесс, протекающий при постоянной температуре называется изотермическим (изос – равный, термо – тепло). Из уравнения состояния идеального газа следует, что при

(7.8)

Давление в изотермическом процессе обратно пропорционально удельному объему.

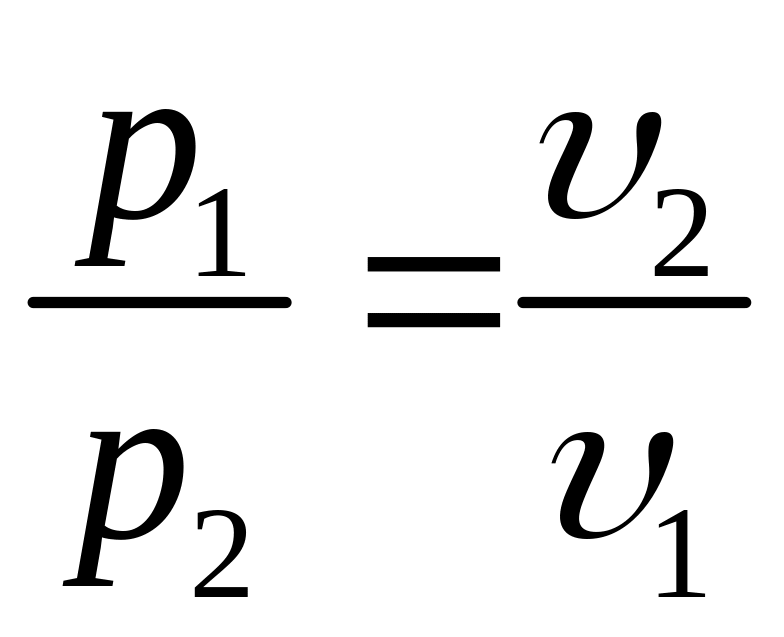(7.9)

В диаграмме (рис. 7.3) уравнение изображается равнобокой гиперболой, в координатах изотермический процесс – прямая линия, параллельная оси абсцисс. Приращение внутренней энергии в процессе не происходит, так как при величина , и следовательно .

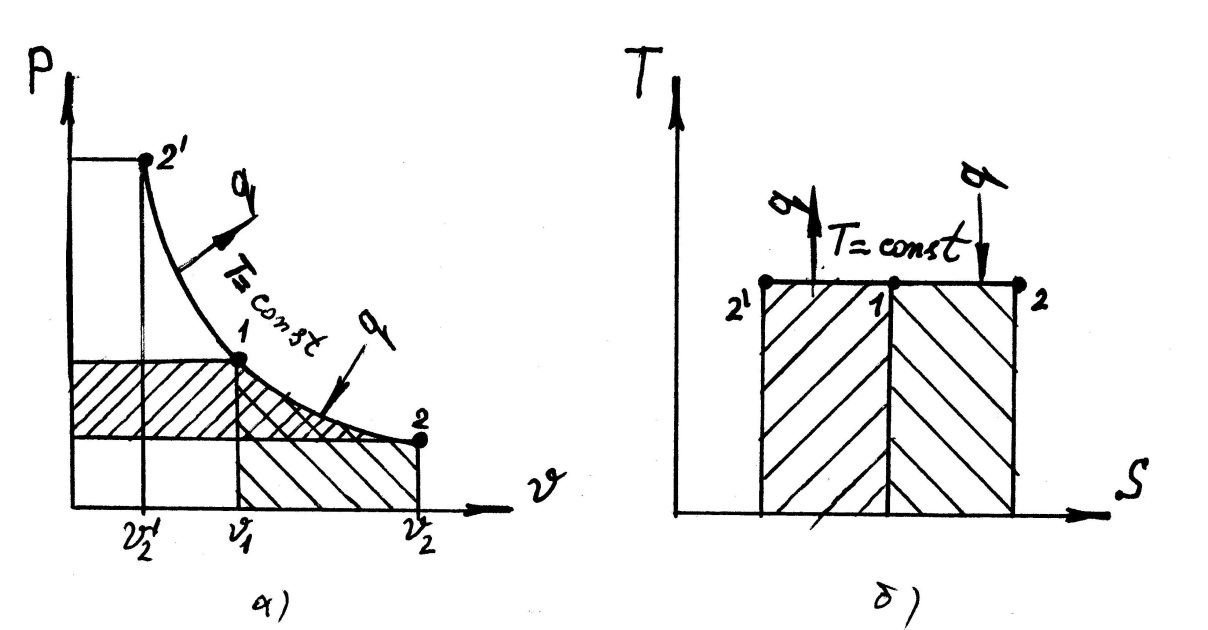
Рис. 7.3 а) рабочая диаграмма изотермического процесса; б) тепловая диаграмма изотермического процесса.

Работа процесса

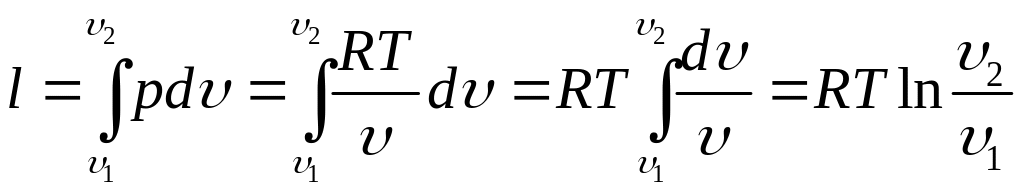(7.10)

Вместо в выражении (7.10) можно подставить . И тогда

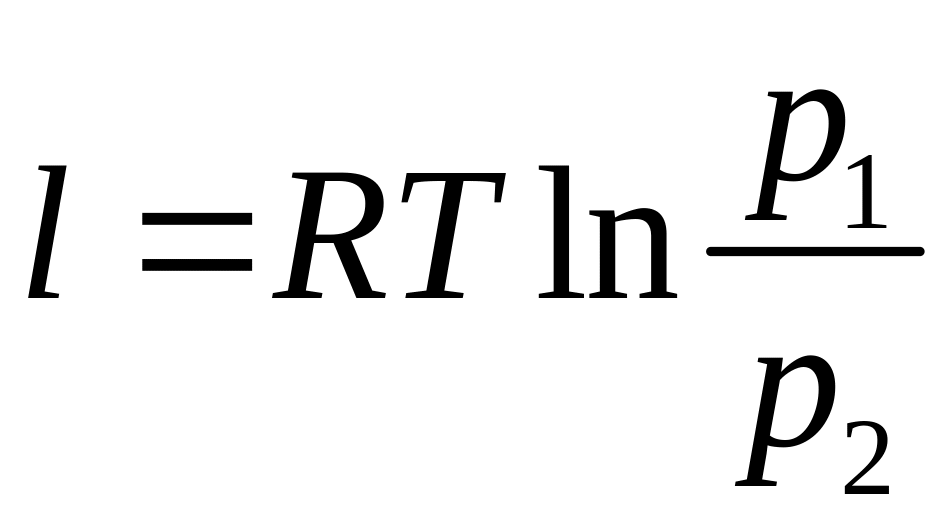(7.11)

Уравнение (7.11) можно представить в виде:

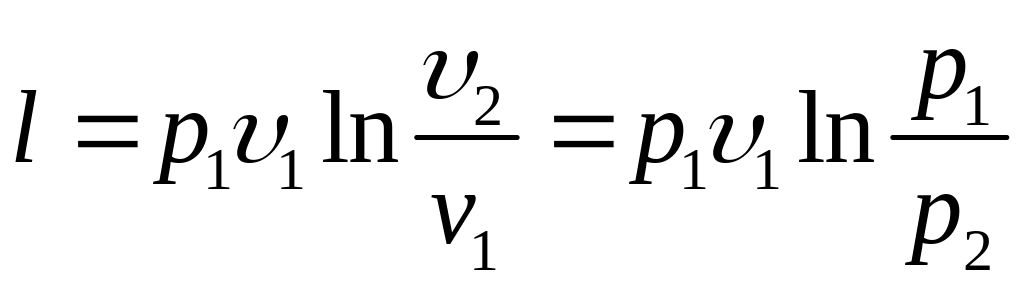(7.12)

Так как приращение внутренней энергии не происходит, то внесенная в процесс теплота трансформируется в работу. С термодинамической точки зрения изотермический процесс является наиболее совершенным процессом.

Адиабатный процесс.

Адиабатным называется процесс, протекающий без теплообмена с окружающей средой. Соответственно, в течении всего процесса . Адиабатными считаются не только процессы, проходящие в хорошо изолированных системах, но и быстротекущие процессы, такие, как сжатие газа в компрессоре, истечение пара со скоростью 1500...2000 м/с на лопатки турбины, расширение газов при выстреле и т.д.

Основное уравнение адиабатного процесса

(7.13)

Здесь – показатель адиабаты, равный отношению изобарной к изохорной теплоемкости

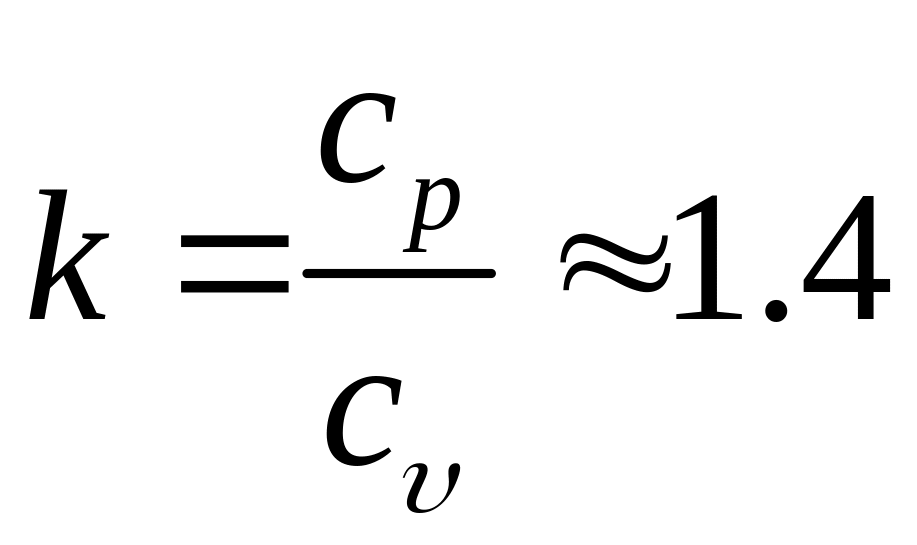(7.14)

Из уравнения (7.13) следует:

.

Откуда

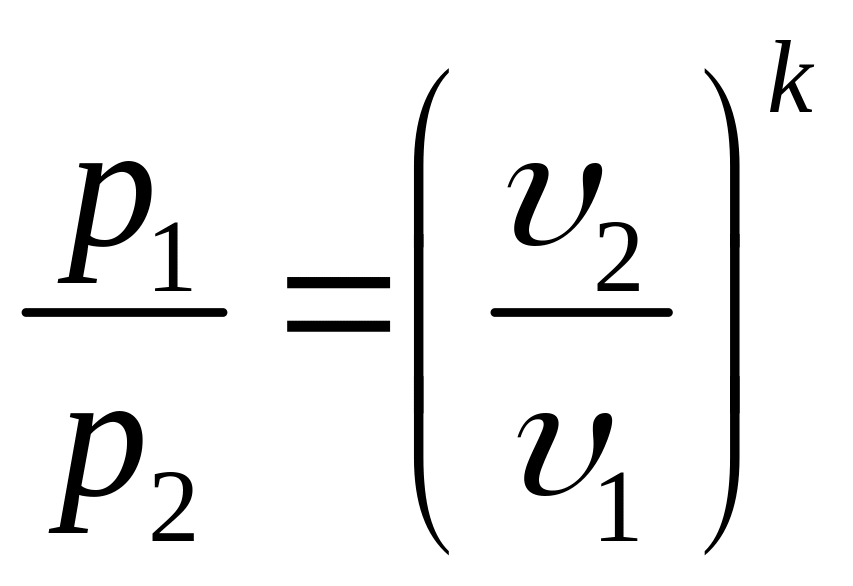(7.15)

либо

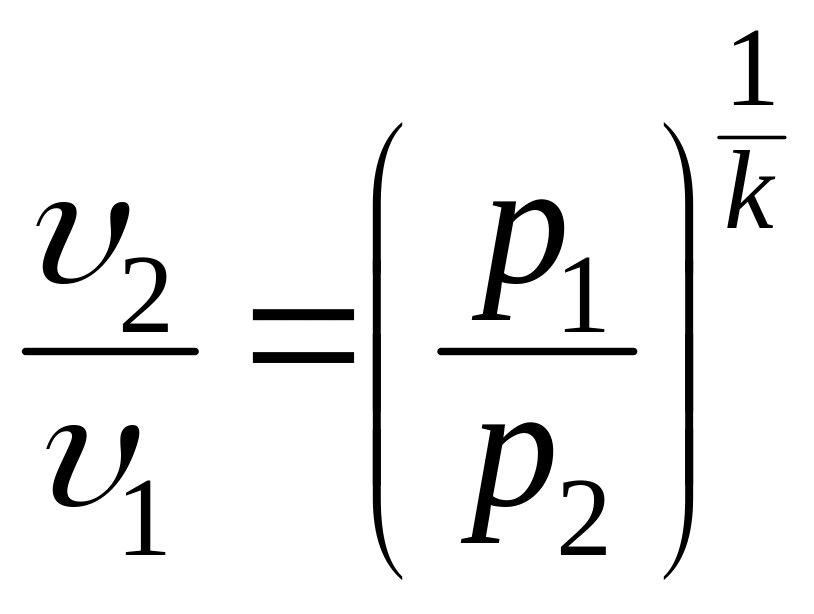(7.15')

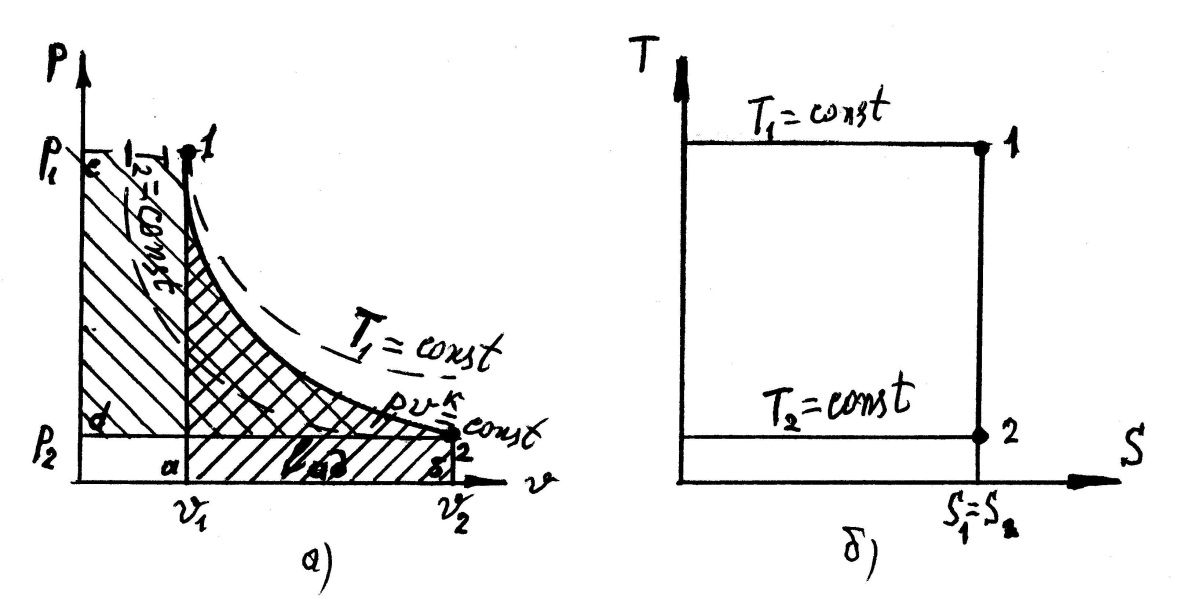
Рис. 7.4 а) рабочая диаграмма адиабатного процесса; б) тепловая диаграмма адиабатного процесса.

На рис. 7.4 показаны рабочая и тепловая диаграмма адиабатного процесса. Из рис. 7.4(а) видно, что работа расширения в адиабатном процессе выражается площадью 1-2-b-a.

Записав характеристическое уравнение для точек 1 и 2 и поделим первое выражение на второе и получим

(7.16)

Воспользуемся выражениями (7.15), (7.15') и подставим их в выражение (7.16)

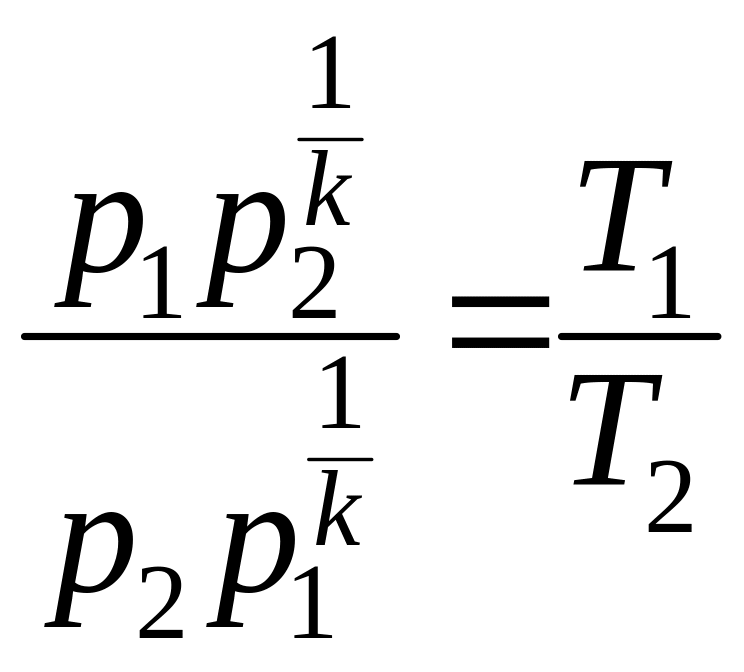и

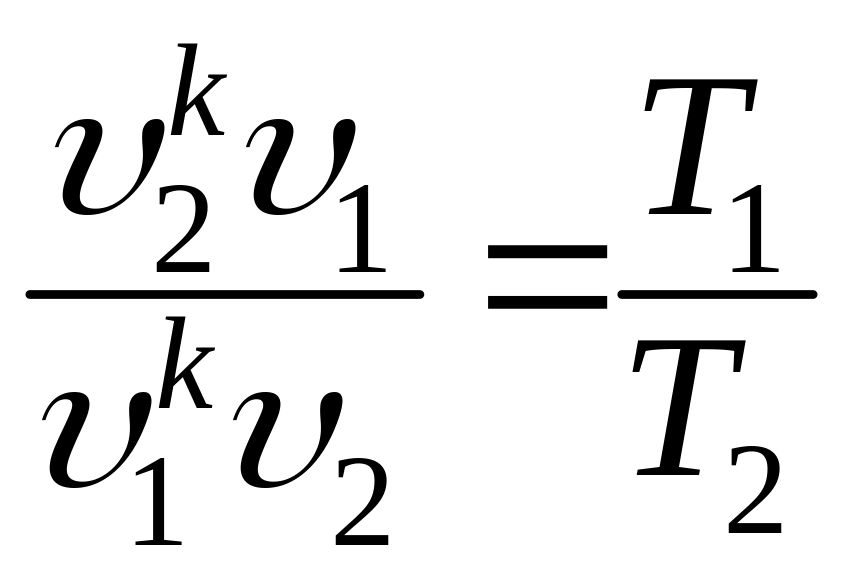
откуда окончательно получим

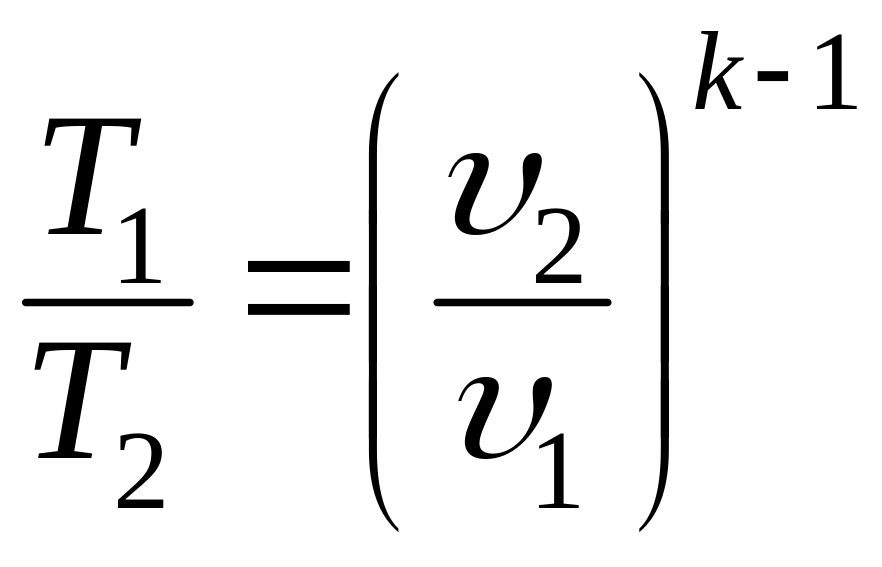и 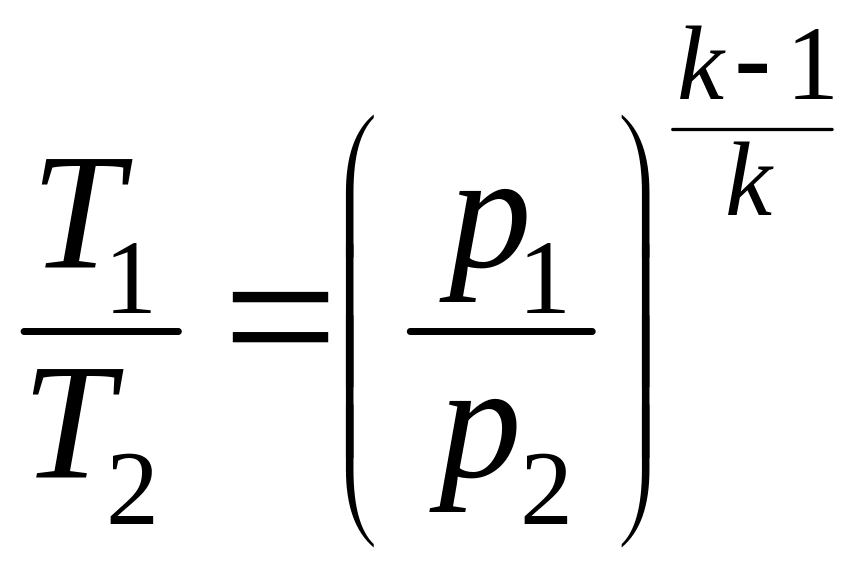(7.17)

Уравнения (7.17) можно представить также в виде:

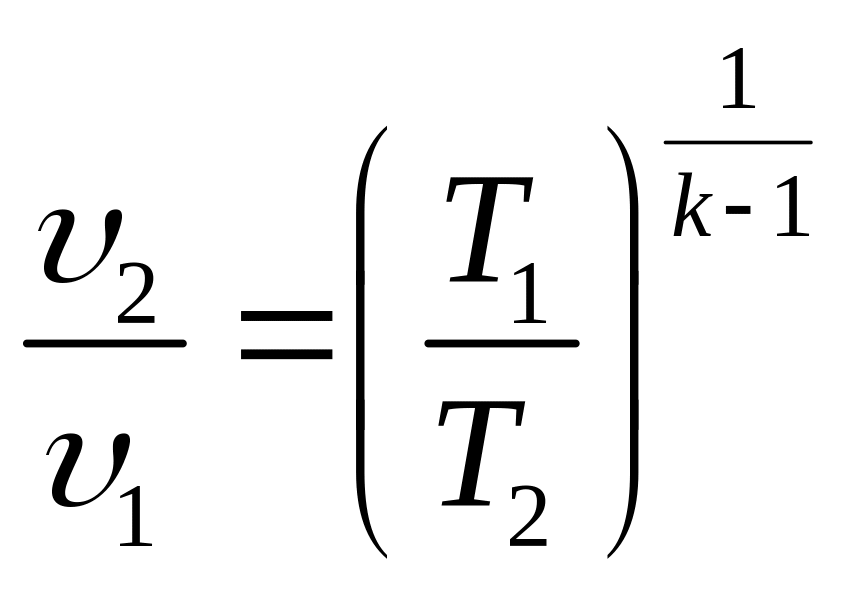и 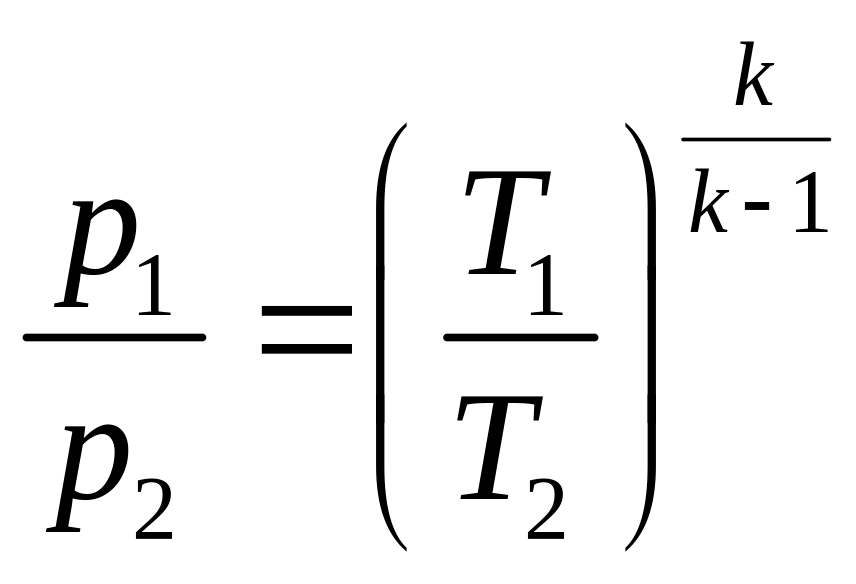(7.18)

Так как адиабатный процесс идет без теплообмена, то все изменение внутренней энергии расходуется на совершение работы

или (7.19)

Используя полученные ранее уравнения и выражение (7.19) можно получить следующие уравнения для расчета работы

(7.20)

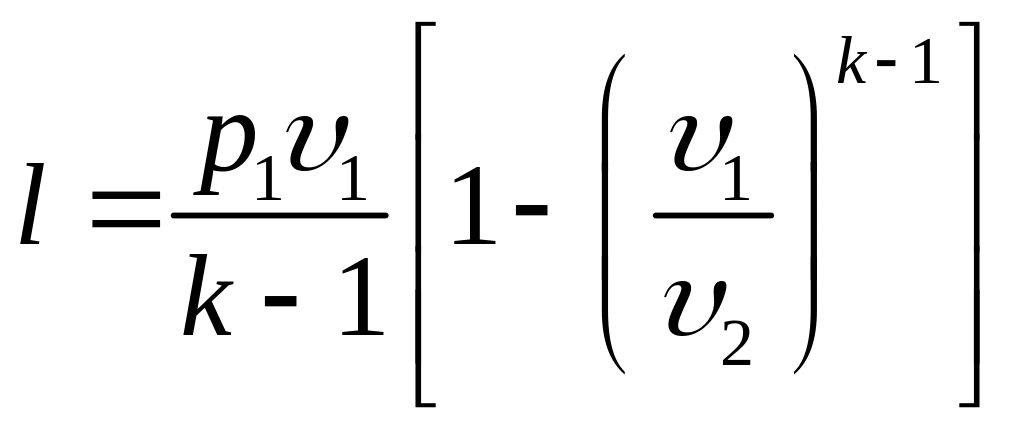(7.21)