6.4. Газовые смеси

В технике часто приходится иметь дело с газообразными веществами близкими по свойствам к идеальным газам и состоящими из механической смеси отдельных газов. Это продукты сгорания ДВС, ГТС, реактивного и других тепловых двигателей. Газовой смесью называется смесь отдельных газов НЕ вступающих между собой в химические реакции. Каждый газ в смеси сохраняет свои свойства и ведёт себя так, как если бы он один занимал весь объём.

Общее давление в газовой смеси складывается из парциальных давлений, которые создаются каждым из компонентов смеси.

Парциальным называется давление, создаваемое одним компонентом на стенки сосуда. Полное (абсолютное) давление по закону Дальтона равно сумме парциальных давлений всех компонентов смеси.

(6.30)

Каждый компонент смеси распространяется по всему объёму со своим парциальным давлением.

Парциальным объёмом называется объём одного компонента, который бы он имел, если бы находился при температуре смеси и своём парциальном давлении.

(6.31)

Уравнение (6.31) иногда называют законом Амага.

Задачей расчёта газовой смеси является определение газовой постоянной или средней молярной массы на основании заданного состава смеси. Все остальные параметры газовой смеси могут быть определены по уравнению Менделеева-Клапейрона (6.22; 6.24).

6.5. Теплоёмкость газа

Чтобы одинаковые массы различных веществ нагреть от одинаковой начальной до одинаковой конечной температуры, необходимо затратить различное количество теплоты. Так на нагревание воды необходимо затратить примерно в 9 раз больше теплоты, чем на нагрев такого же количества железа. Потому что теплоёмкость воды примерно в 9 раз выше теплоёмкости железа.

Теплоёмкостью называют количество тепла, потребное для нагревания единицы количества вещества на один градус.

Средняя теплоёмкость:

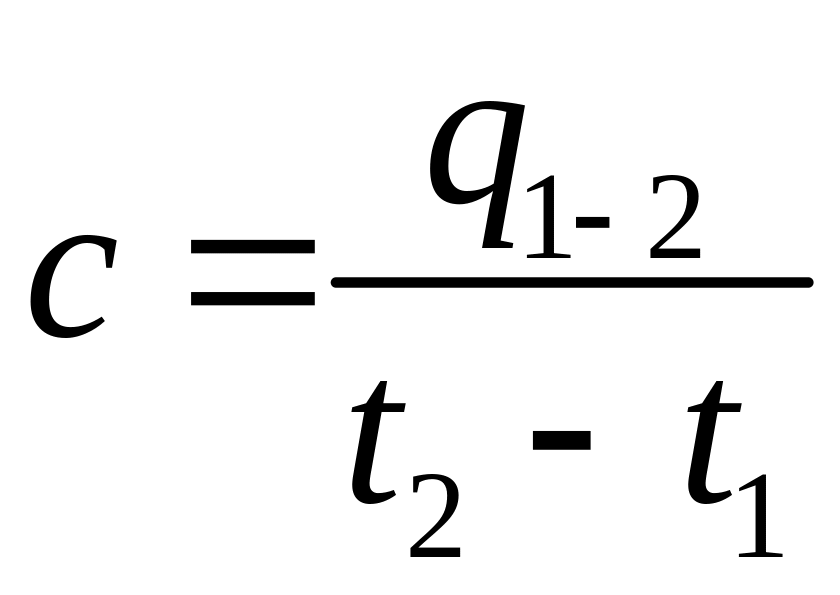(6.32)

где – удельное количество теплоты, затраченное в данном термодинамическом процессе нагревания 1-2.

t_1, t₂ – начальное и конечное значения температуры тела.

Так как количество вещества может быть задано в массовых, объёмных или мольных единицах, различают средние массовую С(кДж/кг*град), объемную С_об(кДж/м³*град), и мольную С_µ(кДж/Кмоль*град) теплоёмкость.

Между этими величинами теплоёмкости существует связь:

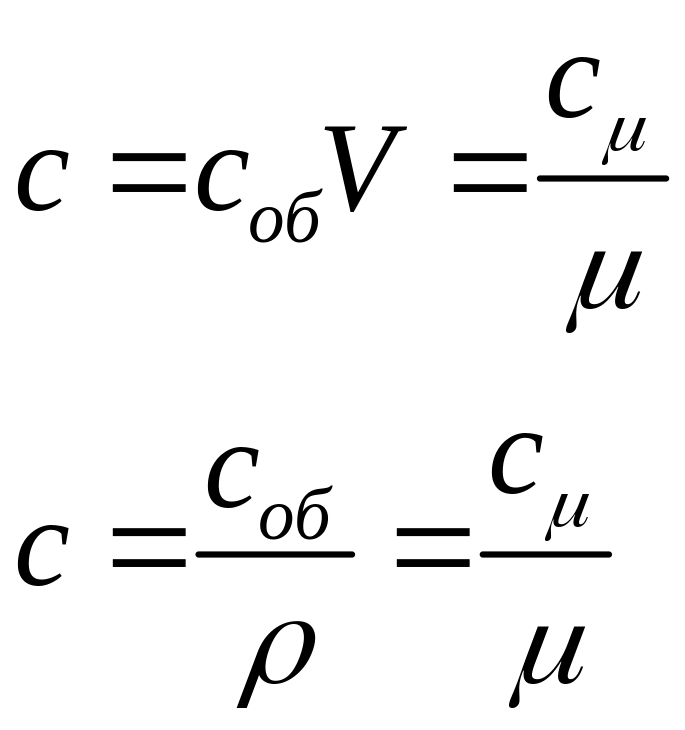(6.33)

Теплоёмкость газов в значительной мере зависит от внешних условий, при которых подводят (или отводят) теплоту. Теплоёмкость газов в термодинамических процессах, происходящих при постоянном удельном объёме называют изохорной и обозначают С_v, а теплоёмкость газов в процессах при постоянном давлении называют изобарной и обозначают С_p.

При изохорном подводе теплоты объём газа не увеличивается и следовательно не совершается работа расширения, т.е. вся теплота идет на увеличение внутренней энергии.

При изобарном процессе нагрева газ расширяется, преодолевая противодействие внешних сил- толкая поршень, т. е. совершая работу. Соответственно, чтобы нагреть газ до одинаковой температуры – при изобарном процессе необходимо затратить больше теплоты, чем при изохорном.

Чтобы убедиться в этом можно в два одинаковых цилиндра поместить по 1 кг одного и того же газа с одинаковыми параметрами. Но, так как поршень одного из цилиндров заклинен, и происходит процесс нагрева газа при V=const, то в этом цилиндре газ нагреется быстрее, получив при этом меньшее количество тепла, которое расходуется только на нагрев газа:

(6.34)

Во втором цилиндре только часть теплоты израсходована на повышение температуры газа от T₁ до T₂, а вторая часть теплоты израсходована на перемещение поршня (на производство работы). То есть газ воспринял больше тепла при нагреве до одной и той же температуры:

(6.35)

На производство работы затрачено количество теплоты:

(6.36)

При изобарном процессе полученную работу можно рассчитать:

(6.37)

Используя уравнение Клапейрона (6.20) для изобарного процесса можно записать:

(6.38)

Сравнивая выражения (6.36) и (6.38) можно записать:

(6.39)

Сократив левую и правую часть на разность температур , получим уравнение закона Майера:

(6.40)

Часто в теплотехнических расчётах используется также соотношение теплоёмкостей . С удовлетворительной точностью применительно ко всем двухатомным газам и воздуху можно считать значения с_p и с_v величинами постоянными и равными с_р= 1,004 кДж/кг*град и с_v = 0,716 кДж/кг*град. Тогда

(6.41)