3.5 Уравнение Бернулли для элементарной струйки идеальной жидкости

Р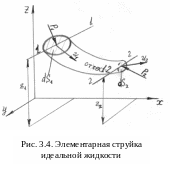 ассмотрим элементарную струйку идеальной жидкости. Выделим в ней отсек 1-2, ограниченный сечениями 1-1 и 2-2. В сечении 1-1 площадью dS₁ (рис.3.4), действует давление p₁, а скорость движения жидкости U₁. В сечении 2-2 – давление p₂, площадь dS₂ , скорость U₂. Центры тяжести выбранных сечений расположены на высотах Z₁ и Z₂ над плоскостью х₀у. Если бы жидкость, расположенная в трубке тока между сече ниями 1-1 и 2-2 былa неподвижна, то можно было бы записать уравнение равновесия жидкости в соответствии с основным уравнением гидростатики

.

или умножив все члены на g, получим

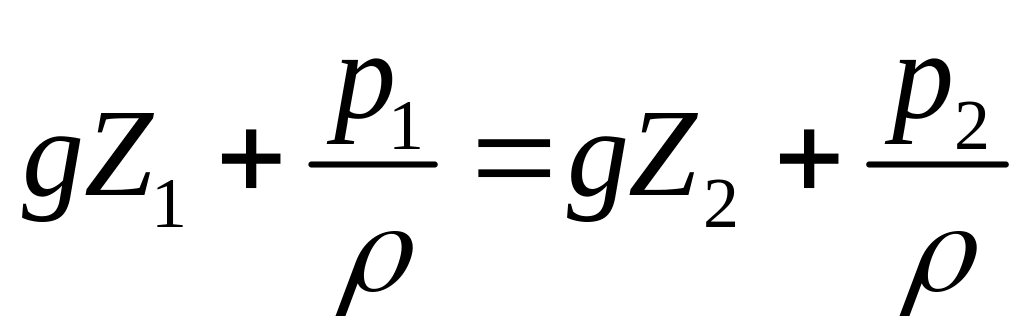. (3.13)

Уравнение (3.13) описывает закон сохранения потенциальной энергии в условиях покоя жидкости. Действительно, если 1 кг жидкости поднять на высоту Z₁ над условной плоскостью сравнения, а под действием давления в этом сечении жидкость в трубке пьезометра сможет подняться еще на высоту , то она обладает суммарной удельной потенциальной энергией единицы массы

Е¹ _пот=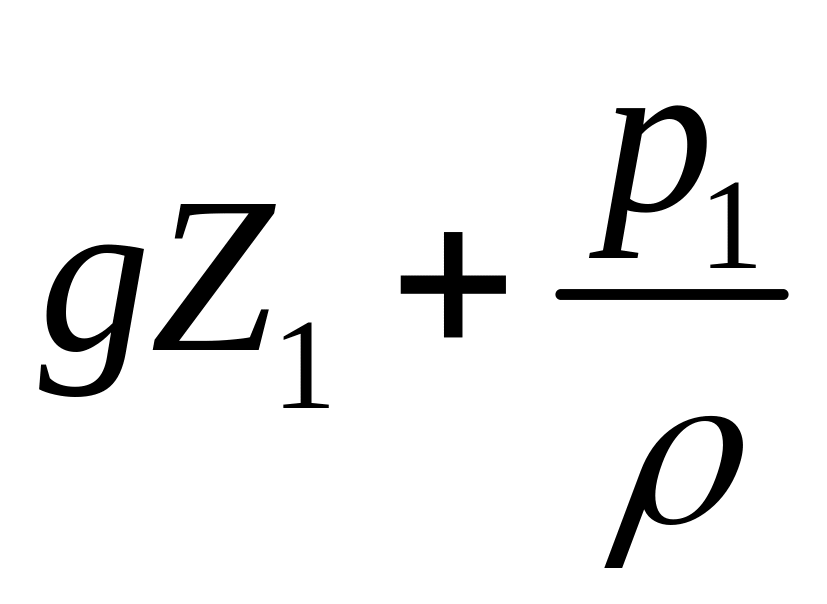 , . (3.14)

При движении жидкость обладает также кинетической энергией. Удельная кинетическая энергия единицы массы жидкости для первого сечения

, . (3.15)

Присоединяя значение кинетической энергии к суммарной потенциальной энергии жидкости в состоянии покоя получим уравнение, характеризующее равновесие жидкости в условиях движения

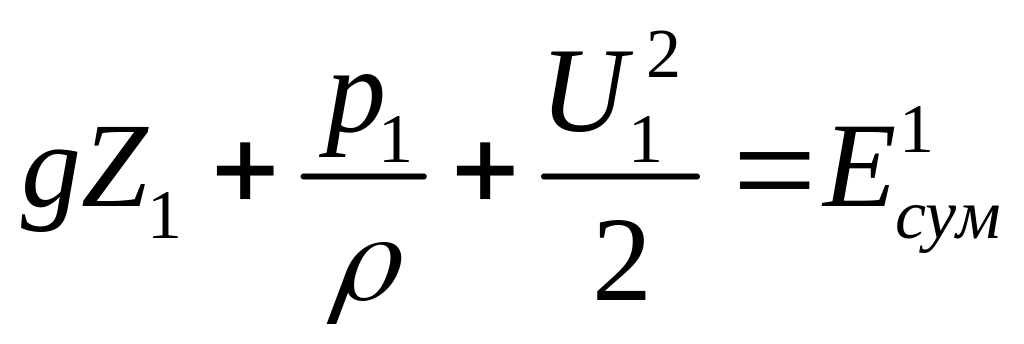, . (3.16)

А так как действует закон сохранения энергии, то можно записать

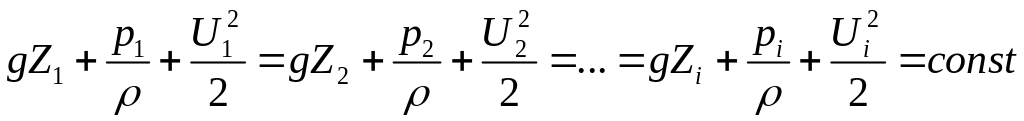. (3.17)

Уравнение (3.17) устанавливает связь между геометрическим положением, давлением и скоростью жидкости в произвольном сечении. Оно называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Анализируя уравнение можно увидеть, что расширение струйки (увеличение площади живого сечения струйки) приводит к уменьшению скорости струйки, а это уменьшает кинетическую энергию. А так как полная энергия струйки в любом сечении является величиной постоянной, т.е. сумма членов является константой, то увеличивается потенциальная энергия давления жидкости в данном сечении. И наоборот, уменьшение площади живого сечения струйки вызывает увеличение скорости и, следовательно, увеличение кинетической энергии, что приводит к уменьшению энергии потенциальной и соответственному падению давления. Проведем анализ размерности всех членов входящих в уравнение (3.17) помня о том, что силы инерции и силы тяжести были отнесены к единице массы жидкости, то есть члены уравнения, в которых присутствует скорость либо ускорение необходимо помножить на .

gZ = = = = .

Мы получили размерность удельной энергии, энергии отнесенной к единице массы жидкости ( – это энергия 1 кг жидкости).

= = = ,

= = = .

Уравнение (3.17) иллюстрирует энергетический смысл уравнения Бернулли – в любом сечении струйка жидкости обладает одной и той же суммарной энергией. Энергия трансформируется переходя из одного вида в другой при изменении условий течения, но сумма потенциальной и кинетической энергии остается постоянной. Рассмотрим еще один вид уравнения Бернулли – вид иллюстрирующий геометрический смысл. Для этого разделим все члены уравнения (3.17) на g

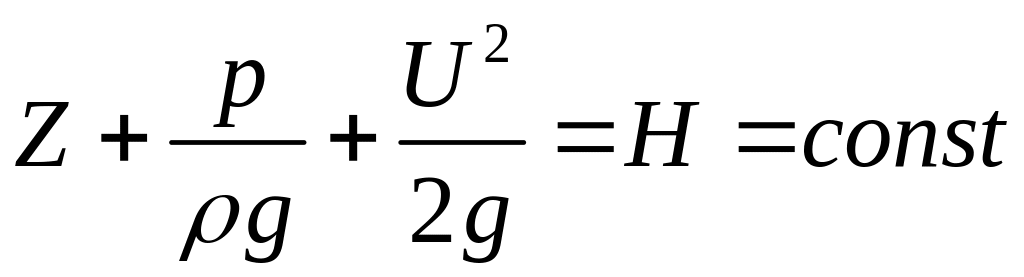. (3.18)

При геометрической интерпретации трактовки уравнения Бернулли все члены уравнения (3.18) могут быть представлены отрезками. Здесь

z – высота положения выбранного сечения над плоскостью сравнения, м;

- пьезометрическая высота или высота, на которую поднимется жидкость под действием давления в заданной точке, если в эту точку поместить пьезометр, м;

- скоростной напор, м;

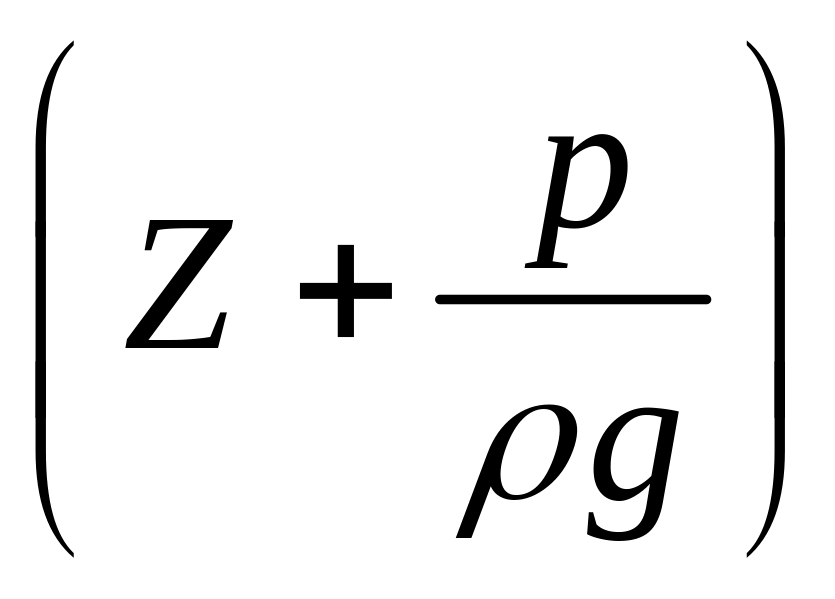- полный гидростатический напор, м;

Н – полный гидродинамический напор, м.

Все члены уравнения (3.18) имеют линейную размерность – м.