3.3 Параметры струйки и потока жидкости

Введем понятия живого сечения и расхода элементарной струйки. Живое сечение элементарной струйки dS_i – это площадь поперечного сечения элемент арной струйки нормального линиям тока. Расходом элементарной струйки (элементарным расходом) называется объемное количество жидкости, проходящее в одну секунду через живое сечение струйки.

Рассмотрим сечение 1-1 элементарной струйки (рис.3.2). В соответствии со свойствами элементарных струек скорость движения одинакова для всех частиц, проходящих через сечение 1-1. За единицу времени из сечения 1-1 частицы жидкости пройдя путь равный скорости движения U₁ , переместятся в сечение 2-2. Через живое сечение элементарной струйки dS₁ за единицу времени пройдет количество жидкости равное объему цилиндра

(3.3)

Это и будет элементарный расход или расход элементарной струйки.

Так как поток состоит из бесконечного количества элементарных струек, то площадь сечения потока будет состоять из суммы площадей живых сечений элементарных струек. Живое сечение потока – это площадь сечения потока, перпендикулярного элементарным струйкам.

Объем жидкости, протекающий в единицу времени через живое сечение потока называется объемным расходом потока или расходом потока

Q = , . (3.4)

Очень важно в гидродинамике понятие средней скорости потока. Понятие средней скорости потока – это чисто условное понятие, математический смысл которого – частное от деления расхода потока на площадь живого сечения потока

V_{ср =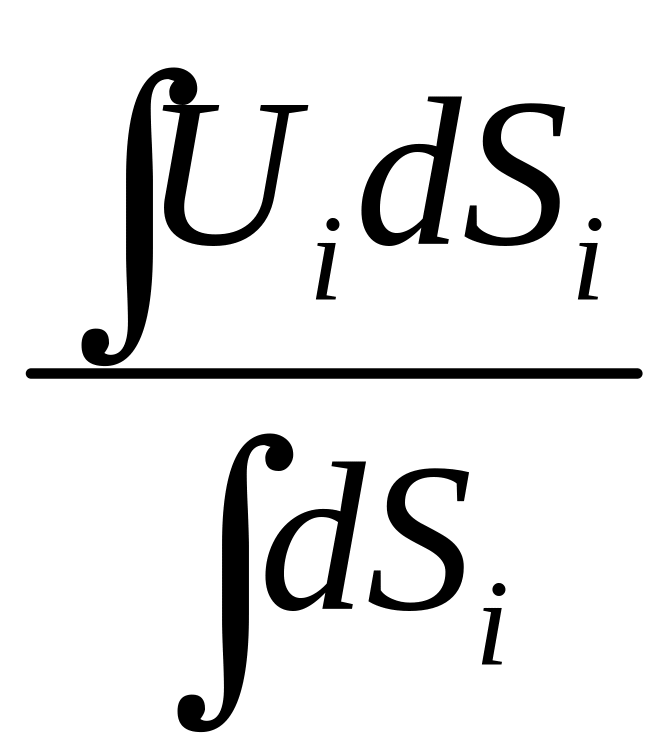} . (3.5)

Средняя скорость потока в живом сечении – это скорость, с которой должны двигаться частицы жидкости через сечение, чтобы получить реальное значение расхода потока.

Из понятия средней скорости потока возникает формула для определения расхода

Q = VS, м³/с, (3.6)

здесь V – средняя скорость движения частиц жидкости через сечение, м/с;

S – площадь живого сечения потока, м².

3.4 Уравнение неразрывности потока

Р ассмотрим элементарную струйку (рис. 3.3), условно разделенную на отсеки сечениями 1-1, 2-2, 3-3, 4-4. Сечения проведены на расстояниях U₁, U₂, U₃, где U_1, U₂, U₃ – скорости движения жидкости в сечениях 1-1, 2-2, 3-3. В отсек 1-2 через сечение 1-1 площадью dS₁ со скоростью U₁ за одну секунду вольется объемное ко-

личество жидкости U₁ ∙dS₁., то есть расход жидкости через первое сечение dQ₁ = U₁ ∙dS₁. Из этого же отсека за единицу времени через сечение 2-2 выльется количество жидкости Q₂ = U₂ ∙dS₂. Причем форма отсека 1-2 не изменилась, а его боковая поверхность непроницаема. Поэтому объем жидкости поступающей в отсек равен объему жидкости, которая из отсека вытекает

U₁dS₁ = U₂dS₂. (3.7)

Аналогично по всем отсекам

U₁ dS₁ = U₂ dS₂ = U₃ dS₃ = …. = U_іdS_і = const = dQ. (3.8)

Уравнение (3.8) является уравнением неразрывности элементарной струйки, которое показывает, что расход жидкости через любое сечение струйки величина постоянная, а струйка неразрывна, так как скорость жидкости не может быть равной нулю при положительном значении dQ. Из уравнения можно получить пропорции для любой пары сечений

(3.9)

Скорости жидкости в произвольной паре сечений обратно пропорциональны площади этих сечений. Для того, чтобы перейти от уравнения неразрывности струйки к уравнению неразрывности потока необходимо проинтегрировать уравнения неразрывности струйки в каждом сечении по площади сечения

. (3.10)

Применяя понятие средней скорости потока в каждом сечении потока можно записать

Q= V₁ S₁= V₂ S₂= …= V_іS_і = const, (3.11)

где V₁ V_2…. V_і – средние скорости жидкости в соответствующих сечениях;

S₁ S_2… S_і – площади сечений.

Уравнение (3.11) является уравнением неразрывности потока жидкости при установившемся движении. Анализируя уравнение легко установить, что любое изменение площади сечения приводит к изменению скорости в этом сечении.

Для потока также можно составить пары пропорций для любых сечений, например

. (3.12)