11. Доверительные границы случайной погрешности
При измерениях практический интерес представляет нахождение доверительного интервала (– Δr, + Δr), в котором с заданной доверительной вероятностью РΔ находится измеряемая величина хи = 0,95. Аналитически доверительную вероятность удобно записать в следующем виде:
Границы доверительного интервала принято указывать симметричными относительно результата измерения. При технических измерениях доверительную вероятность устанавливают РД = 0,95. Если используется нормальный закон распределения, то поиск доверительного интервала выполняют с помощью значений интеграла вероятностей Ψ(z). При этом задают доверительную вероятность РД и по табл. 2.1 находят значение параметра z, соответствующее Ψ(z) = РД. Далее, учитывая z и заранее вычисленную оценку СКО результата измерения, определяют доверительную границу случайной погрешности:
Аналитически нижнюю Ан и верхнюю Ав границы доверительного интервала представляют в следующем виде: Ан=z ; Ав= +z
При одинаковой доверительной вероятности с уменьшением числа наблюдений доверительный интервал увеличивается, т. е. точность измерений снижается.
12.Суммирование случайных и систематических погрешностей.
По характеру проявления выделяют погрешности:
систематическую (коррелированную) θ – погрешность, которая может оставаться постоянной или закономерно изменяться при повторных измерениях одной и той же постоянной величины. Эту погрешность можно выявить и устранить, введя поправки в измерения. Она обусловлена несовершенством средств измерения, метода измерения, влиянием внешних условий измерений (температура, влажность, избыточное давление), органов чувств наблюдателя. Устраняется очередной поверкой прибора, установкой нуля, использованием стабилизированного источника питания, а также устраняется, если для измерения ФВ применять метод замещения, метод противопоставления, метод двух отсчетов и метод рандомизации. По причинам возникновения ее подразделяют на методическую, инструментальную, дополнительную и погрешность взаимодействия;
случайную (некоррелированную) – погрешность, изменяющаяся случайным образом (по знаку и величине) при повторных измерениях одной и той же постоянной величины, проведенных с одинаковой тщательностью. Их закономерности можно выявить при больших количествах измерений (например, 24), избежать их невозможно. Причиной появления может быть нестабильность переходного сопротивления в контактах, трение в опорах, влияние гистерезиса, изменение освещенности, усталость глаз, неточность установки линейки, неточность установки начала отсчета, влияние магнитных и электрических промышленных помех. Систематическая и случайная погрешности проявляются одновременно;
При проведении многократных измерений случайная погрешность может быть уменьшена во много раз. Однако погрешность усредненного результата будет определяться не этой весьма малой случайной погрешностью, а не зависящей от числа усредняющих отсчетов систематической погрешностью.
Механизм суммирования систематической и случайной составляющих погрешности отличается от механизма суммирования случайных погрешностей. Согласно ГОСТ 8.207—76 погрешность результата измерения определяется по следующим правилам. Если границы неисключенной систематической погрешности 6 и оценка СКО результата измерения Sсвязаны соотношением
то следует пренебречь систематической составляющей погрешности и учитывать только случайную погрешность результата. При этом доверительные границы погрешности результата ∆ = tpS, где tp — коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа проведенных измерений п. Если же имеет место неравенство
то, наоборот, следует пренебречь случайной составляющей и результат характеризовать лишь границами его суммарной систематической погрешности ∆ = Ѳ. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности, при выполнении указанных неравенств не превышает 15%.
Числа 0,8 и 8 в стандарте никак не обосновываются. Однако если принять во внимание, что, как было показано ранее, ∆0,9= 1,6S, то условие (9.16) эквивалентно неравенству Ѳ < ∆0 9/2. Условие (9.17) эквивалентно неравенству Ѳ > 5∆0,9. Следовательно, ГОСТ 8.207-76 разрешает пренебрегать систематической составляющей и учитывать только случайную составляющую лишь тогда, когда она в 2 раза превышает систематическую. Если же случайная составляющая менее 1/5 систематической, ею можно пренебречь.
При невыполнении неравенств (9.16) и (9.17) границу суммарной погрешности ГОСТ 8.207-76 предписывает находить путем композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины. Допускается границы погрешности результата измерений определять по формуле
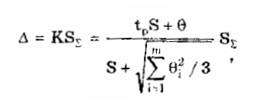
где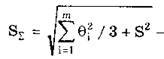
-
оценка суммарного СКО суммарной
погрешности.
Данный подход, приводящий к заниженным оценкам, вызывает [4] справедливые нарекания и вряд ли его следует считать правомочным. Рассмотрим этот вопрос подробнее.
Систематическая
погрешность, присутствующая во всех
отсчетах, не усредняется при статистической
обработке. На рис. 9.1 показаны истинное
значение измеряемой величины хи,
границы систематической погрешности Ѳ,
распределение случайной составляющей
погрешности р(х). Из рисунка ясен механизм
суммирования составляющих погрешности.
Если систематическая составляющая
постоянна, то ее модуль |Ѳ| должен
суммироваться с доверительным интервалом
случайной составляющей tpS,
а отнюдь не с СКО. Доверительный интервал
суммарной погрешности
Из рис. 9.1 становятся понятными рассмотренные выше условия, при которых можно пренебречь одной из составляющих суммарной погрешности. На рис. 9.1,а показана ситуация, когда нельзя пренебречь ни одной из составляющих. На рис. 9.1,6 доверительный интервал случайной составляющей более чем в два раза больше систематической составляющей, и последней можно пренебречь. На рис. 9.1,в систематическая составляющая превышает доверительный интервал случайной составляющей более чем в 5 раз, и ее также можно не учитывать при определении суммарной погрешности.
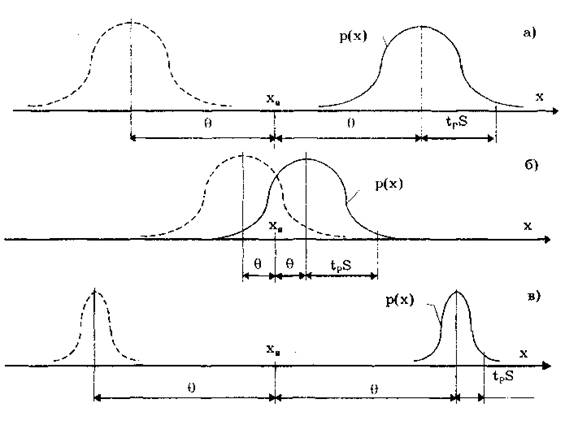
Рис. 9.1. Систематическая и случайная составляющие погрешности