Полярные координаты. Связь полярных и декартовых координат. Уравнение кривой второго порядка в полярных координатах.
Полярная
система координат – двумерная система
координат, в которой каждая точка на
плоскости определяется двумя числами
– полярным углом и полярным радиусом.
Связь полярных и декартовых координат:
прямоугольные координаты точки
через её полярные координаты:
полярные
координаты точки
через её прямоугольные координаты:
///
– полярный радиус;
– полярный угол;
– полюс;
– полярная ось. Координаты точки
записываются так:
/Уравнение
кривой второго порядка в полярных
координатах:
где
,
,
Декартовы координаты. Преобразования системы координат (параллельный перенос, поворот). Деление отрезка в заданном отношении.
Декартовой
обычно
называют прямоугольную систему координат
с одинаковыми масштабами по осям.
Прямоугольная
система координат
– прямолинейная
система
координат
с
взаимно перпендикулярными осями на
плоскости или в пространстве.
Преобразования
системы координат: параллельный перенос
//
. поворот системы координат
//
; Деление отрезка в заданном отношении.
//
//
//
//
//
//
Понятие о множествах и их элементах. Подмножества. Операции над множествами: объединение, пересечение, разность. Равенство множеств. Пустое и универсальное множество.
Под
множеством понимают совокупность
некоторых объектов, объединенных по
какому-либо признаку. Объекты, из которых
состоит множество, называются его
элементами. Множества принято обозначать
заглавными буквами латинского алфавита
,
а их элементы – малыми буквами
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
символом Ø. Универсальное множество –
такое множество, которое состоит из
элементов, в также подмножеств множества
объектов исследуемой области. Множество
называется подмножеством множества
,
если каждый элемент множества
является элементом множества
.
Символически это обозначается так
.
Говорят, что множества
и
равны или совпадают, и пишут
,
если
и
.
Другими словами, множества, состоящие
из одних и тех же элементов, называются
равными. Объединением (или суммой)
множеств
и
называется множество, состоящее из
элементов, каждый из которых принадлежит
хотя бы одному из этих множеств.
Объединение (сумму) множеств обозначают
(или
).
Кратко можно записать
.
Пересечением (или произведением)
множеств
и
называется множество, состоящее из
элементов, каждый из которых принадлежит
множеству
и множеству
.
Пересечение (произведение) множеств
обозначают
(или
).
кратко можно записать
.
Декартово произведение двух и более множеств. Бинарные и n-арные отношения. Свойства бинарных отношений.
Отображения одного множества в другое, область определения и область значений, график отображений. Композиция (суперпозиция) отображений. Взаимно однозначные отображения. Обратное отображение.
Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу xϵX сопоставляет один и только один элемент yϵY, называется функцией и записывается y=f(x), xϵX или f:X→Y. Говорят еще, что функция f отображает множество X на множество Y. Отображение множества X в множество Y - соответствие, в силу которого каждому элементу х множества X соответствует определённый элемент у = f (x) множества.
Множество X называется областью определения функции f и обозначается D(f). Множество всех yϵY называется множеством значений функции f и обозначается E(f).
Пусть задана функция y=f(x) с областью определения D и множеством значений E. Если каждому значению yϵУ соответствует единственное значение xϵD, то определена функция x ϵ φ(y) с областью определения E и множеством значений D. Рис.
Такая
функция φ(y)
называется обратной к функции f(x)
и записывается как: x=φ(y)=
(y).
Функции y=f(x)
и x
ϵ
φ(y)
взаимно обратные. Чтобы найти функцию
x
ϵ
φ(y),
обратную функции y=f(x),
надо решить уравнение f(x)=y
относительно x.
Пусть
функция y=f(u)
определена на множестве D,
а функция u=φ(x)
на множестве
,
причем для x
соответствующее значение u=φ(x)
ϵD.
Тогда на множестве
определена функция u=f(φ(x)),
которая называется сложной функцией
от x
(или суперпозицией заданных функций).
Переменную u=φ(x)
называют промежуточным аргументом
сложной функции.
Множество натуральных чисел. Метод математической индукции. Элементы комбинаторики. Перестановки, сочетания, размещения в выборках с повторением и без повторения.
Бином Ньютона.
Множество действительных чисел.
Функция одной действительно переменной. Числовые (скалярные) функции как отображения множеств. Основные свойства функций. Способы задания функции. Сложные и обратные функции.
Понятие числовой последовательности. Предел числовой последовательности. Теоремы о пределе последовательности.
Критерий Коши сходимости числовой последовательности. Теорема Вейерштрасса.
Арифметические свойства пределов (сумма, разность, произведение и частное пределов последовательности).
Бесконечно малые и бесконечно большие последовательности, их свойства.
Предел функции в точке и на бесконечности. Теоремы о пределе функции. Арифметические свойства пределов функции (сумма, разность, произведение и частное двух функций).
Число
называется пределом функции в точке
(или при
),
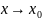если для любого положительного
найдется такое положительное число
,
что для всех
,
удовлетворяющих неравенству
,
выполняется неравенство
.
Коротко определение выглядит так:
Число
называется пределом функции
при
,
если для любого положительного числа
существует такое число
,
что при всех
,
удовлетворяющих неравенству
выполняется неравенство
.
Коротко определение выглядит так:
Теоремы о пределе функции. Арифметические свойства пределов функции.
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Доказательство:
Пусть
,
.
Тогда по теореме о связи функции, её
предела и б.м.ф. можно записать
и
.
Следовательно,
.
Здесь
– б.м.ф. как сумма б.м.ф. По теореме о
связи функции, её предела и б.м.ф. можно
записать
,
т.е.
Теорема 2. Предел произведение двух функций равен произведению их пределов:
Доказательство:
Пусть
,
,
то
,
,
где
и
– б.м.ф. Следовательно,
т.е.
Выражение в скобках есть б.м.ф. Поэтому
т.е.
Теорема 3. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
Доказательство:
Из
равенств
и
следуют отношения
и
.
Тогда
Второе слагаемое есть б.м.ф. как частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел. Поэтому:
т.е.
