41.Метод моментов.

Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: , учитывая, что получим , как видно из соотношения

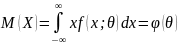
есть функция от , поэтому можно рассматривать как уравнение с одним неизвестным . Решив это уравнение относительно параметра , тем самым найдем его точечную оценку 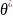, которая является функцией от выборочной средней, следовательно, и от вариант выборки: .

Для отыскания двух параметров необходимыдва уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моментувторого порядка:

учитывая что 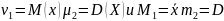получим:

Математическое ожидание и дисперсия есть функции от θ1 и θ2, поэтому можно рассматривать как систему двух уравнений с двумя неизвестными θ1 и θ2. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценки. Эти оценки являются функциями от вариант выборки.

42.Метод максимального правдоподобия.

Функцией правдоподобия дискретной случайной величины X называют функцию аргумента .

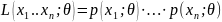
В качестве точечной оценки параметра принимают такое его значение , при котором функция правдоподобия достигает максимума. Оценку θ* называют оценкой наибольшего правдоподобия.

Функцией правдоподобия непрерывной случайной величины X называют функцию аргумента θ: .

Оценку наибольшего правдоподобия неизвестного параметра

распределения непрерывной случайной величины ищут так же, как в случае дискретной величины.

43.Точечная оценка математического ожидания и среднего квадратического отклонения для нормального закона распределения.

44.Свойства точечных оценок.

Пусть   — случайная выборка из распределения, зависящего от параметра  . Тогда статистику  , принимающую значения в  , называют точечной оценкой параметра 

Свойства точечных оценок

Оценка   называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности: ,

где   обозначает математическое ожидание в предположении, что   — истинное значение параметра (распределения выборки  ).

Оценка   называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

Оценка   называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:  ,  по вероятности при  .

Оценка   называется сильно состоятельной, если  ,

 почти наверное при  .

45.Точечная оценка для математического ожидания.

Точечной оценкой для математического ожидания в силу закона больших чисел является выборочное среднее арифметическое  . В некоторых случаях могут быть использованы и другие оценки. Например, если известно, что распределение симметрично относительно своего центра, то центр распределения является не только математическим ожиданием, но и медианой, а потому для его оценки можно использовать выборочную медиану.

          Нижняя доверительная граница для математического ожидания имеет вид

 – U(p) s0 / n1/2 ,

где:            – выборочное среднее арифметическое,          p – доверительная вероятность (истинное значение   математического ожидания находится между нижней       доверительной границей и верхней доверительной границей с           вероятностью, равной доверительной);

          U(p) – число, заданное равенством Ф(U(p)) = (1+ p)/2, где Ф(х) –        функция стандартного нормального распределения с     математическим ожиданием 0 и дисперсией

  Верхняя доверительная граница для математического ожидания имеет вид  + U(p) s0/ n1/2 .

46.Интервальная оценка математического ожидания для нормального закона распределения в случае известного .

Гмурман «Руководство по решению задач...» стр. 174

47.Интервальная оценка математического ожидания для нормального закона распределения в случае неизвестного .

Гмурман «Руководство по решению задач...» стр. 174

48. Точечная оценка дисперсии

49.Интервальная оценка дисперсии для нормального закона распределения.

50. Проверка гипотез: классификация гипотез

Проверку гипотез на основе выборочных статистических данных называют статистической проверкой гипотез. Можно дать следующее определение:

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

При проверке гипотез, как правило, выделяют основную ( или нулевую) гипотезу и обозначают её , а другую – в качестве альтернативной и обозначают .

Различают гипотезы, которые содержат одно и более одного предположений.

Простой называю гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Можно рассмотреть простоту гипотез и с другой точки зрения: гипотеза - простая если ей соответствует одно распределение или одна точка пространства параметров, и сложная, если она сводится к выбору какого-либо распределения из целого множества или точке из интервала.

51.Проверка гипотез: основные понятия.

Процедура сопоставления высказанной гипотезы с выборочными данными называется проверкой гипотезы.

Этап 1. Располагая выборочными данными  и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Но, которую называют основной или нулевой, и гипотезу Н₁ конкурирующую с гипотезой Н₀. Термин «конкурирующая» означает, что являются противоположными следующие два события:

• по выборке будет принято решение о справедливости для генеральной совокупности гипотезы Н₀;

• по выборке будет принято решение о справедливости для  генеральной совокупности гипотезы Н₁.Гипотезу H₁ называют также альтернативной.

Этап 2. Задаются вероятностью  , которую называют уровнем значимости. Поясним ее смысл.Решение о том, можно ли считать высказывание Н₀  справедливым для генеральной совокупности, принимается по выборочным данным, т. е. по ограниченному ряду наблюдений, следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов:

• отвергают гипотезу Но, или, иначе, принимают альтернативную гипотезу H₁, тогда как на самом деле гипотеза Н₀ верна; это ошибка первого рода;

• принимают гипотезу Н₀ , тогда как на самом деле высказывание Но неверно, т. е. верной является гипотеза Н₁  это ошибка второго рода.

Этап 3. Находят величину  такую, что:

ее значения зависят от выборочных данных, т. е. для которой справедливо равенство

-         ее значения позволяют судить о «расхождении выборки с гипотезой Н₀»;

-         и которая, будучи величиной случайной в силу случайности выборки, подчиняется при выполнении гипотезы Но некоторому известному закону распределения.Величину   называют критерием.

Этап 4. Далее рассуждают так. Так как значения критерия позволяют судить о «расхождении выборки с гипотезой Но», то  из области допустимых значений критерия  следует выделить подобласть  таких значений, которые свидетельствовали бы о существенном расхождении выборки с гипотезой Но и, следовательно, о невозможности принять гипотезу Но.

52.Проверка гипотезы о равенстве дисперсии заданной величине.

53.Проверка гипотезы о равенстве математического ожидания заданной величине.

54.Проверка гипотезы о равенстве дисперсий двух нормально распределенных выборок.

55 Выборочный коэффициент корреляции.

В качестве измерителей степени тесноты парных связей между количественными переменными используются коэффициент корреляции (или то же самое "коэффициент корреляции Пирсона") и корреляционное отношение.

Выборочный коэффициент корреляции находится по формуле

где   - выборочные средние квадратические отклонения величин   и  .

Выборочный коэффициент корреляции   показывает тесноту линейной связи между   и  : чем ближе  к единице, тем сильнее линейная связь между   и  .