33.Свойства математического ожидания.
Математическое ожидание постоянной равно этой постоянной
Постоянную величину можно выносить за знак математического ожидания, то есть если С – постоянная, а Х – случайная величина, то
Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин
Математическое ожидание произведения случайных величин равно произведению их математических ожиданий плюс корреляционный момент.
Математическое ожидание суммы
это
случайная величина, принимающая
целочисленные значения.
34.Свойства дисперсии.
Дисперсия постоянного равна нулю
Доказательство:
Если
- постоянное, то
Доказательство:
Дисперсия суммы независимых случайных величин равна сумме их дисперсий:
Доказательство:
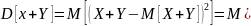
Величины
x
иy
независимы, поэтому
.
35.Неравенство Чебышева.
Пусть
имеется случайная величина
с математическим ожиданием
и
дисперсией
.
Каково бы ни было положительное число
,
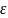вероятность того, что величина
отклонится от своего математического
ожидания не меньше чем на
,
ограничена сверху числом
36.Теорема Чебышева.
Пусть
имеется
бесконечная
последовательность независимых случайных
величин с одним и тем же математическим
ожиданием
и
с дисперсиями ограниченными одной и
той же постоянной:
,
тогда каково бы ни было
,
вероятность события
стремится
к 1 при
.
37.Теорема Бернулли.
–
число
наступлений события в
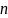независимых попытках,
-
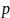вероятность появления события в одном
опыте.
38.Центральная предельная теорема.
Если
независимые случайные величины, имеющие
один и тот же закон распределения с
математическим ожиданием m
и дисперсией D,
то при неограниченном увеличении n
закон распределения суммы
неограниченно приближается к нормальному.
39.Предмет и задачи математической статистики.
Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных. Любая наука решает в порядке возрастания сложности и важности следующие задачи:
описание явления;
анализ и прогноз;
поиск оптимального решения.
Такого рода задачи решает и математическая статистика:
систематизировать полученный статистический материал;
на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины;
определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения.
Одной из задач третьего типа является задача проверки правдоподобия гипотез.
40.Понятие генеральной и выборочной совокупностей.Эмпирический закон распределения.
Генеральной
совокупностью называется вероятностное
пространство
и
определенная на этом пространстве
случайная величинаX.
Случайной выборкой или просто выборкой
объема n
называется последовательность
,
n
независимых одинаково распределенных
величин, распределение каждой из которых
совпадает с распределением исследуемой
случайной величины X.
Выборку часто называют эмпирическим
рядом.