25.Непрерывные классические распределения.

Равномерное распределение. Непрерывная случайная величина х имеет равномерное распределение в интервале [a,b], если на этом интервале плотность распределения случайной величины постоянна, а вне его равна нулю.

Нормальное распределение. Нормальным распределением называется распределение непрерывной случайной величины х с параметрами и , плотность распределения которой имеет вид

Показательное распределение. Непрерывная случайная величина х распределена по показательному закону, если ее плотность распределения имеет вид

, где - параметр распределения, который называют интенсивностью отказов.

26.Определение многомерной случайной величины.

n-мерной случайной величиной или случайным вектором называется упорядоченный набор nслучайных величин X=(X1,…,Xn)Множество точек на n-мерной плоскости называется бореловским, если оно может быть получено из множества вида применением конечного или счетного числа операций объединения и дополнения.

27.Функция распределения вероятностей для многомерных случайных величин.

Функция распределения -мерной случайнойвеличины определяется формулой

Свойства: неубывающая, непрерывная слева. Удовлетворяет соотношениям:

при любом

при любом

28.Законы распределения, производные от нормального закона распределений.

29.Математическое ожидание случайной величины.

Математическое ожидание является числовой характеристикой, которая характеризует положение случайной величины на числовой оси, поэтому иногда ее называют характеристикой положения.

Математическим ожиданием дискретной случайной величины X, заданной таблицей

		…
		…

называется сумма ряда

если ряд сходится абсолютно.

Если задана непрерывная случайная величина X и p(x) – ее плотность распределения, то математическим ожиданием величины X называется интеграл

30.Дисперсия и среднее квадратическое отклонение случайной величины.

Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной величины. .

Дисперсия имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобней пользоваться величиной, которая есть квадратный корень из дисперсии 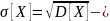среднее квадратическое отклонение.

31.Моменты случайной величины.

Начальным моментом s-го порядка дискретной случайной величины X называется сумма вида

Для непрерывной случайной величины X начальным моментом s-го порядка называется интеграл

Центральным моментом порядка s случайной величины X называется математическое ожидание s-й степени соответствующей центрированной случайной величины

32.Числовые характеристики системы случайных величин.

Математическим ожиданием n-мерной системы случайных величин называется совокупность n интервалов.

Дисперсией n-мерной случайной величины называется совокупность постоянных, определяемых формулой:

Величина есть дисперсия величины , то есть

Характеристику , при , называют корреляционным моментом. Корреляционный момент характеризует рассеивание величин и связь между ними.

Для независимых величин корреляционный момент равен 0.