1.Предмет теории вероятностей.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, как было уже сказано, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений герба, если монета будет брошена достаточно большое число раз. При этом 'предполагается, конечно, что монету бросают в одних и тех же условиях.

Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.

В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.

2.Статистическое определение вероятности.

Классическое определение не требует проведения опыта. В то время как реальные прикладные задачи имеют бесконечное число исходов, и классическое определение в этом случае не может дать ответа. Поэтому в таких задачах будем использовать статическое определение вероятностей, которое подсчитывают после проведения эксперимента или опыта.

Статической вероятностью w(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний. w(A)=m/n

Относительная частота события обладает свойством устойчивости:

Lim(n→∞)P(∣m/n−p∣<ε)=1 (свойство устойчивости относительной частоты)

3.Классическое определение вероятностей.

ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:P(A)=m/n

где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.

4.Аксиоматическое определение вероятности.

Пусть - множество элементов , которые называются элементарными событиями, а - множество подмножеств множества , называемых случайными событиями, а – пространством элементарных событий. Сформулируем аксиомы, определяющие вероятность.

1 аксиома (алгебра событий). Множество является алгеброй событий.

2 аксиома (существование вероятности событий). Каждому событию из множества поставлено в соответствие неотрицательное действительное число 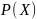, которое называется вероятностью события .

3 аксиома (нормирование вероятности).

4 аксиома (аддитивность вероятности). Если события не пересекаются, то

5.Размещения с повторениями. Размещением с повторениями из n элементов по m называют любой кортеж длины rm составленный из элементов n-членного множества X.  Число всех таких размещений обозначается и выражается формулой Данная формула непосредственно следует из правила произведения.