25. Теоремы Лагранжа и Каши. Формула конечных приращений Лагранжа.

конечных приращений формула формула Лагранжа, одна из основных формул дифференциального исчисления, дающая связь между

приращением функции f(x) и значениями еѐ производной, эта формула имеет вид: f(b)-f(a)=(b-a)f’(c),

где с — некоторое число, удовлетворяющее неравенствам a<с<b.< em=""> Формула (1) справедлива,

если функция f(x) непрерывна на отрезке [a,b] и имеет производную в каждой точке интервала

(а, b).</b.<>

Теорема Лагранжа Если функция y=f(x):

1). Определена и непрерывная на всем сегменте [a; b]; 2). Производная f ′ (x) ограничена на этом сегменте;

Тогда на интервале (a; b) есть хотя бы одно число c которое удовлетворяет следующему равенству: f(b) -f(a)=(b-a) ⋅ f ′ (c) c ∈ (a; b).

Теорема Коши Если функции f(x) и g(x):

1). Определены и непрерывны на всем сегменте [a; b];

2). Производные g′ (x), f ′ (x) ограничены на этом сегменте;

3). (g′ (x))²+ (f ′ (x))² ≠ 0, для всех x∈ (a; b); 4). g(a) ≠ g(b);

Тогда на интервале (a; b) существует хотя бы одно число c которое удовлетворяет следующему равенству:

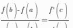, c ∈ (a; b).

26. Монотонность функции. Достаточный признак возрастания (убывания) функции. Достаточные признаки экстремума функции одного переменного.

Монотонность функции

Возрастающие и убывающие функции объединяют общим понятием: монотонные функции.

Монотонная функция – это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Говоря иначе, если при возрастании значения x значение y тоже возрастает, то это возрастающая функция. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Говоря иначе, если при возрастании значения x значение y убывает, то это убывающая функция.

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.Функция постоянна (немонотонна), если она не убывает и не возрастает.

формулировки признаков:

если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

найти область определения функции; найти производную функции; решить

неравенства и на области определения; полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

27. Формула Тейлора. Остаточный член формулы Тейлора.

• Представление простых элементарных функций по формуле Тейлера.

• Рассмотрим функцию . Все еѐ производные совпадают с ней: , так что коэффициенты Тейлора в точке равны

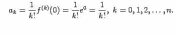
Поэтому формула Тейлора для экспоненты такова:

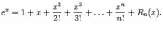
2. Рассмотрим функцию 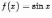. Еѐ производные чередуются в таком порядке: формулу Тейлора для синуса:

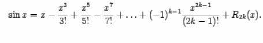
разложение косинуса по формуле Тейлора имеет вид