
- •3) Понятие функции, область определения функции.
- •6) Тригонометрические функции. Обратные тригонометрические функции.
- •8) Предел функции в точке.
- •9) Свойства предела функции в точке.
- •14.Сравнение бесконечно малых
- •21. Правила дифференцирования (производные сложной и обратной функции).
- •22. Дифференцируемость функции. Дифференциал одной переменной, его геометрический смысл.
- •23. Производные и дифференциалы высших порядков. Формула Лейбница.
- •24. Экстремум функции одного переменного, необходимое условие экстремума (теорема Ферма), Теорема Ролля.
- •25. Теоремы Лагранжа и Каши. Формула конечных приращений Лагранжа.
- •26. Монотонность функции. Достаточный признак возрастания (убывания) функции. Достаточные признаки экстремума функции одного переменного.
- •27. Формула Тейлора. Остаточный член формулы Тейлора.
- •29. Выпуклость функции. Точки перегиба. Необходимые и достаточные условия существование точек перегиба.
- •30. Асимптоты графика функции. Уравнение асимптоты вертикальной и наклонной.
- •41)Теорема о среднем в определённом интеграле.
- •42) Интеграл с переменным верхним пределом.
- •43) Формулы замены переменной и интегрирования по частям для определенного интеграла.
- •44) Несобственные интегралы
- •45) Несобственные интегралы. Условия сходимости интегралов.
21. Правила дифференцирования (производные сложной и обратной функции).
(производная обратной функции).
Пусть
y=f(x) - функция от аргумента x в некотором
интервале(a,b) . Если в уравнении y=f(x) y
считать аргументом, а x - функцией, то
возникает новая функция
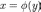 , где
, где
 - функция обратная данной.
- функция обратная данной.
Теорема (о дифференцировании обратной функции)
Для
дифференцируемой функции с производной,
отличной от нуля, производная обратной
функции равна обратной величине
производной данной функции, т.е

Пример 1. Найти x'y, если y = 2x3+3x5+x Имеем y' = 6x2+15x4+1, тогда x'y = 1/y'x = 1/(6x2+15x4+1).
(дифференцирование сложной функции).

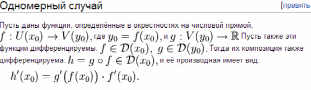

Пример 5. Найти y', если y = 5cos x. y' = 5cos x(-sin x)ln 5=-5cos x sin x ln 5.
22. Дифференцируемость функции. Дифференциал одной переменной, его геометрический смысл.
Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.
. Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Геометрический смысл дифференциала
Построим график функции y = f (x). В точке M(x, f (x)) проведем касательную MT. Как известно, tg α = f ' (x), из Δ ТМР имеем TP = MP· tg α, MP = Δ x = dx, поэтому
TP = f '(x)·dx = dy.
Дифференциал функции есть приращение ординаты касательной.
Замечание.
Из определения дифференциала следует,
что производная функции равна отношению
дифференциала функции к дифференциалу
ее аргумента
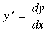
23. Производные и дифференциалы высших порядков. Формула Лейбница.
Пусть
функция
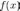 определена на
определена на
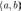 и дифференцируема в каждой точке этого
интервала. Тогда на интервале
определена функция
и дифференцируема в каждой точке этого
интервала. Тогда на интервале
определена функция
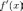 .
Пусть функция
дифференцируема
в некоторой точке
.
Пусть функция
дифференцируема
в некоторой точке
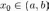 ,
то есть
,
то есть
 .
Тогда эта производная называется
производной второго порядка функции
в точке
.
Тогда эта производная называется
производной второго порядка функции
в точке
 .
.
 ;
;
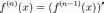
Теорема
(формула Лейбница). Пусть
 и
и
 в точке
в точке
 .
Тогда в этой точке
.
Тогда в этой точке

Пусть
функция
 задана и дифференцируема на некотором
интервале
задана и дифференцируема на некотором
интервале
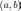 ,
тогда
,
тогда
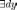 для
для
 ,
причем
,
причем
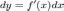 .
Заметим, что функция
.
Заметим, что функция
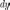 - это функция двух переменных
и
- это функция двух переменных
и
 .
Рассмотрим функцию
как функцию переменной
(фиксируем
).
.
Рассмотрим функцию
как функцию переменной
(фиксируем
).
Пусть
имеет производную в некоторой точке
 .
Тогда функция
имеет
дифференциал в точке
.
.
Тогда функция
имеет
дифференциал в точке
.
Определение.
Дифференциалом
второго порядка в точке
называется дифференциал от дифференциала
первого порядка в этой точке и обозначается:
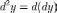
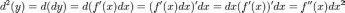
Аналогично
определим дифференциа любого порядка.
Пусть функция
 дифференцируема
дифференцируема
 раз на интервале
и
раз на интервале
и
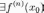 для некоторой точки
.
для некоторой точки
.
Определение.
Дифференциалом
порядка
 функции
функции
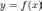 в точке
называется дифференциал от дифференциала
порядка в этой точке и обозначается:
в точке
называется дифференциал от дифференциала
порядка в этой точке и обозначается:
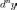

24. Экстремум функции одного переменного, необходимое условие экстремума (теорема Ферма), Теорема Ролля.
Теорема
Ролля.. Пусть: Функция
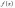 непрерывна на отрезке
непрерывна на отрезке
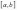 :
:
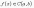 ;
Для любого x из интервала
;
Для любого x из интервала
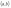 существует производная:
существует производная:
 ;Значения
функции на концах отрезка равны:
;Значения
функции на концах отрезка равны:
 .
Тогда существует такое
.
Тогда существует такое
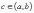 ,
что производная
,
что производная
 .
.
Доказательство
Функция
непрерывна
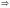 существуют
существуют
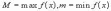 .Если
.Если
 ,
то функция
,
то функция
 является константой, и ее производная
в любой точке равна 0, т.е. теорема
доказана.Если же
является константой, и ее производная
в любой точке равна 0, т.е. теорема
доказана.Если же
 ,
то оба значения
,
то оба значения
 не могут достигаться в концевых точках,
т.к.
не могут достигаться в концевых точках,
т.к.
 и
.
и
.
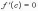
Тогда хотя бы одно из них достигается во внутренней точке c, и, по теореме Ферма
Пусть функция f (х) определена на отрезке [a;bJ и во внутренней точке Хо этого отрезка принимает оптимальное (максимальное или минимальное значение) значение. Пусть в точке Хо существует производная f'(хо). Тогда f'(хо) = о.
Доказательство.
Предположим противное - пусть Хо - точка экстремума функции f (х), и пусть f'(Хо) Ф о. Рассмотрим для определѐнности случай, когда Хо - точка минимума; предположим, что f'(Хо) > о, тогда слева от точки Хо по теореме о связи знака производной с возрастанием и убыванием функции должно выполняться неравенство f (х) < f (хо), что противоречит предположению о том, что Хо - точка минимума. Если мы предположим, что
f'(Xq) < 0, то справа от точки Xq должно быть верным неравенство f (х) < f (xо), чего также не может быть. Таким образом f'(Xq) = 0, что и требовалось доказать.
