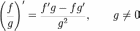14.Сравнение бесконечно малых

Определения

Допустим, у нас есть бесконечно малые при одном и том же x--->a величины a(x) и b(x) (либо, что не важно для определения, бесконечно малые последовательности).

Если , то b — бесконечно малая высшего порядка малости, чем a . Обозначают b=0(a) .

Если , то b — бесконечно малая низшего порядка малости, чем a . Соответственно a=0(b) .

Если (предел конечен и не равен 0), то a и b являются бесконечно малыми величинами одного порядка малости.

Это обозначается как b=O(a) или a=O(b) (в силу симметричности данного отношения).

Если (предел конечен и не равен 0), то бесконечно малая величина b имеет m-й порядок малости относительно бесконечно малой a .

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Если , то бесконечно малые величины a и b называются эквивалентными (a~b).

15. Непрерывность. f непрерывна в точке x₀, если f имеет предел в точке x₀, и этот предел совпадает со значением функции f(x₀). Разрывы: если оба односторонних предела суще. и конечны, но хотя бы один из них не равен значению функции в данной точке, то такую точку называют точкой разрыва первого рода; если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

16. Св-ва непрерывных ф-ий. Если функции f и g непрерывны в точке a, то функции f+g и f*g тоже непрерывны в точке a.

17. Cв-ва функций непрер. на отрезке. Первая теорема Вейерштрасса: Функция, непрерывная на отрезке, ограничена на этом отрезке. Вторая теорема Вейерштрасса: Всякая непрерывная функция ограничена и достигает своей верхней и нижней грани.

 Теорема: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

Первая теорема Больцано–Коши: Если функция f(x)- непрерывна на [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0. Вторая теорема Больцано – Коши: Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

18. Производная.

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.

19.Касательная к графику функции, уравнение касательной и нормали к кривой.

Уравнение касательной: f_l(x)=f(x₀)+f’(x₀)(x-x₀)

Касательной прямой к графику функции в точке называется график линейной функции, задаваемой уравнением.

f_l(x)=f(x₀)+f’(x₀)(x-x₀)

Уравнение нормали к кривой (x-xi) = -(y-yi)*dY/dx; или (x-xi)*dFx/dt = -(y-yi)*dFy/dt;

20. Праивила дифферинцирования (производная суммы произведения и частного)