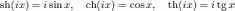1) Числовые множества. Числа вида N = {1, 2, 3, ....} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов.

Числа вида: Z = {... -3, -2, -1, 0, 1, 2, 3, ....} называются целыми числами, т.е. целые числа - это натуральные числа, числа, противоположные натуральным, и число 0.

Целые и дробные числа составляют множество рациональных чисел: Q = Z U {}, где m - целое число, а n - натуральное число.

Числа не являющиеся целыми или дробными называются иррациональными.

Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел: рациональных и иррациональных.

Ограниченные и не ограниченные числовые множества.

Числовое множество Х называется ограниченным , если существует такое число M , что для всех элементов х € Х выполняется неравенство | x | ≤ M

Числовое множество Х называется неограниченным , если какое бы (большое) М мы ни взяли, обязательно найдѐтся элемент х € Х , что будет| x | > M

Понятие точной верхней и нижней грани числовых множеств.

Число M называется верхней гранью числового множества {x}. Аналогично, число m называется нижней гранью числового множества {x}.

Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества {x} (обозначение sup{x}).

Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества {x} (обозначение inf{x}).

2) Числовая последовательность. Числовой последовательностью называется упорядоченное счетное множество чисел {x1, x2, x3, ... }.

Обратите внимание на два момента.

1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность!

2. Все числа упорядочены, то есть расположены в определенном порядке.

Предел последовательности. Число a называется пределом последовательности {xn} при n стремящимся к бесконечности, если .

Для этого факта используют следующие обозначения:

Свойства пределов последовательностей. Постоянный множитель c можно выносить за знак предела:

Если существуют конечные пределы последовательностей {xn} и {yn} , то

Предел линейной комбинации

Предел произведения

Предел частного

3) Понятие функции, область определения функции.

Функция – это одно из основных математических и общенаучных понятий, выражающих зависимость между переменными величинами. Переменную х называют независимой переменной или аргументом. Все значения независимой переменной образу-

ют область определения функции.

Обратная функция. Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией.

Характеристики поведения функций:

Функция является четной, если y(-x) = y(x). Четность функции указывает на симметрию графика относительно оси ординат. ( y = |x|, y = , y = cos x)

Функция является нечетной, если y(-x) = -y(x). Нечетность функции указывает на симметрию графика относительно начала координат. (y = 1/x, y = , y = sin x, y = tg x, y = ctg x, y = arcsin x, y = arctg x)

Возрастание и убывание. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1).

Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1).

Наибольшее и наименьшее значение - понятия математического анализа. Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке функция не имеет большего (меньшего) значения.

Ограниченность. Функция называется ограниченной снизу, если существует R такое, что , .

Функция называется ограниченной сверху, если существует R такое, что , .

Функция, ограниченная сверху и снизу, называется ограниченной.

Периодичность. Функция , определенная на множестве D, называется периодической, если существует число такое, а) что для любого значения и тоже принадлежат D; б) . Число при этом называют периодом функции.

4)Показательные и логарифмические функции. Показательной функцией называется функция вида f(x) = , где основание a — положительная константа.

Функция, обратная к показательной функции f(x) = при a≠0 называется логарифмической функцией по основанию a и обозначается .

Экспоненциальная функция, функция f(x) = , то есть показательная функция. Обозначается также f(x) = exp х.

5) Степенная функция. Степенной функцией с вещественным показателем a называется функция y = , x >0.

Обратная степенная функция.

Свойства степенной функции.

Область определения функции - промежуток (0; + ).

Область значений функции - промежуток (0; + ).

Для любых a график функции проходит через точку (1; 1).

Функция строго монотонно возрастает в области определения функции, то есть, если x1 < x2 то < ( > .)

График степенной функции при a > 0(a < 0) изображен на рисунке.

6) Тригонометрические функции. Обратные тригонометрические функции.

Функции sinx, cos х, tgx, ctgx называются тригонометрическими функциями. Кроме четырех указанных функций, иногда рассматриваются еще две (секанс и косеканс):

Косинус — четная функция: cos (- х) = cos х; синус, тангенс и котангенс —

нечетные: sin(-х) = - sinх, tg(-х) = - tgх, ctg(-х) = -ctg х.

Функции sinx и cos х — периодические с наименьшим положительным периодом T = 2π, так как sin(х + 2πk) = sinx и cos(х + 2πk) = cosх, k ϵ Z. Функции tgx и ctgх — периодические с наименьшим положительным периодом Т = π, так как tg(x + πk) = tgх, ctg (х + πk) = ctg х, k ϵ Z.

Обратные тригонометрические функции.

Арксинусом(arcsin) числа m называется такое значение угла x, для которого

Функция y = sin x непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsin x является строго возрастающей.

Арккосинусом(arccos) числа m называется такое значение угла x, для которого

Функция y = cos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей.

Арктангенсом(arctg) числа m называется такое значение угла альфа, для которого

Функция y = arctg x непрерывна и ограничена на всей своей числовой прямой. Функция y = arctg x является строго возрастающей.

Арккотангенсом(arcctg) числа m называется такое значение угла x, для которого

Функция y = arcctg x непрерывна и ограничена на всей своей числовой прямой. Функция y = arcctg x является строго убывающей.

7) Гиперболические функции. Гиперболические функции, функции, определяемые формулами:

гиперболический синус.

гиперболический косинус.

гиперболический тангенс.

Обратные Гиперболические функции (ареа-синус гиперболический и ареа-косинус гиперболический) определяются формулами:

Связь с тригонометрическими функциями.

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.