Задача № 8

Мебельная фабрика выпускает шкафы и столы. При изготовлении этой продукции требуются сосновые и березовые доски. Для изготовления стола требуется 0,15 м³ сосновых досок и 0,2 м³ березовых, а для изготовления шкафа – 0,2 м³ и 0,1 м³ соответственно. Доски сосновые могут поступать на фабрику в количестве не более 60 м³ в сутки, а березовые – не более 40 м³ в сутки. Прибыль от реализации одного стола –

12 000 Руб, шкафа – 15 000 руб. Составьте план производства мебели, чтобы прибыль от ее реализации была наибольшей.

Математическая модель задачи

Где – количество шкафов и столов соответственно, – максимальная прибыль фабрики.

Система ограничений

Левая часть	Знак	Правая часть
60	<=	60
40	<=	40

Где имеют неотрицательные значения, а данная модель является линейной.

После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения

X1	X2
240	80

Целевая функция:

4560000

= = = >

max

Анализ результатов

Для того чтобы фабрика получила максимальную прибыль от продажи своей продукции, равную 4560000руб, необходимо выпустить 240 шкафов и 80 столов.

Задача № 9

Заводы автомобильной фирмы MG расположены в Лос-Анджелесе, Детройте и Новом Орлеане. Основные центры распределения продукции сосредоточены в Денвере и Майами. Объемы производства указанных трех заводов равняются 1000, 1500 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимость перевозки по железной дороге одного автомобиля на одну милю равняется примерно 8 центам. Расстояния в милях между заводами и центрами распределения приведены в следующей таблице:

	Денвер	Майами
Лос-Анджелес	1000	2690
Детройт	1250	1350
Новый Орлеан	1275	850

Найти опорный и оптимальный планы .

1 миля=1,523 км

переводной коэффициент = 0,08 долл./миля

Предположим, что перевозки автомобилей с завода Детройт в Денвер нежелательны. Каким образом это условие можно включить в модель?

Математическая модель задачи

,

Заводы фирмы MG	Центы распределения			Объёмы произв-ва
	Денвер	Майами
Лос-Анджелес	80	215,2	1000
Детройт	100	108	1500
Новый Орлеан	102	68	1200
Квартальный спрос, в автомобилях	2300	1400			3700
			3700

Где c_ij – это стоимость перевозки одной единицы груза с i-го исходного пункта в j-й пункт назначения, а x_ij – объем перевозимого груза по данному маршруту, то c_ijx_ij – это стоимость перевозки груза по маршруту i-й исходный пункт – j-й пункт назначения. Сложение стоимостей перевозок по всем возможным маршрутам образует стоимость общего плана перевозок.

,

где m – количество исходных пунктов (в рассматриваемой задаче количество заводов);

n – количество пунктов назначения (в рассматриваемой задаче количество центров распределения);

a_i – количество (объем ) груза в i-м исходном пункте;

b_j – количество (объем) груза, которое должно быть завезено в j-й пункт назначения.

Для рассматриваемой задачи имеем:

,таким образом, она является сбалансированной.

Система ограничений

Так как запасы равны потребностям, то все запасы будут вывезены, а все потребности будут удовлетворены. Данные условия можно записать в виде следующих уравнений:

,

,

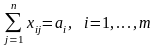Так как количество перевозимого груза не может принимать отрицательные значения, то в рассматриваемой задаче имеет место условие неотрицательности, т. е.:

.

Таким образом система ограничений имеет вид:

1)

лев.часть (вывезено)	знак	прав.ч (запас)
1000	=	1000
1500	=	1500
1200	=	1200

Лев. Ч (завезено)	2300	1400
знак	=	=
прав.ч (потребность)	2300	1400

Данная модель является линейной.

После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения

Заводы фирмы MG	Центры распределения		Уравнения (неравенства)
	Денвер	Майами	лев.часть (вывезено)	знак	прав.ч (запас)
Лос-Анджелес	1000	0	1000	=	1000
Детройт	1300	200	1500	=	1500
Новый Орлеан	0	1200	1200	=	1200
Лев. Ч (завезено)	2300	1400
знак	=	=
прав.ч (потребность)	2300	1400
Стоимость перевозки:			313200	= = = >	min

F= 313200

Анализ результатов

В результате запросы обоих центров удовлетворены в полном объеме при минимальных затратах на транспортировку в размере 313200$, с заводов вывезены все запасы автомобилей. Денверский центр распределения получил 1000 и 1300 автомобилей от заводов в Лос-Анджелесе и Детройте соответственно, а центр распределения, расположенный в Майами, получил 200 и 1200 автомобилей от заводов в Детройте и Новом Орлеане соответственно.