Задача № 6
Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 фунта азотных, 4 фунта фосфорных и 1 фунт калийных удобрений, а в улучшенный – 2 фунта азотных, 6 фунтов фосфорных и 3 фунта калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3 $, а улучшенный – 4 $. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?
Математическая модель задачи
Где – количество обычных и улучшенных наборов удобрений соответственно, - минимальная стоимость наборов удобрений, достаточных для эффективного питания почвы.
Система ограничений
Левая часть |
знак |
Правая часть |
10 |
>= |
10 |
20 |
>= |
20 |
8 |
>= |
7 |
Где имеют неотрицательные значения, а данная модель является линейной.
После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения
X1 |
X2 |
2 |
2 |
Целевая функция: |
14 |
= = = => |
min |
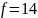
Анализ решения
Для того чтобы минимальные расходы на удобрение, количества которого достаточно для эффективного питания почвы, составляли 14$ необходимо купить 2 набора обычных и 2 набора улучшенных удобрений.
Задача № 7
На ферме в качестве корма для животных используются два продукта: M и H. Сбалансированное питание предполагает, что каждое животное должно получать в день не менее 200 калорий, причем потребляемое при этом количество жира не должно превышать 14 единиц. Подсчитано, что в одном килограмме каждого продукта содержится:
в продукте M –150 калорий и 14 единиц жира;
в продукте H – 200 калорий и 4 единицы жира.
Как разработать максимально дешевый рацион откорма животных, отвечающий этим условиям, если стоимость 1 кг продукта M составляет 1,5 $ , а 1 кг продукта H – 2,5 $?
Математическая модель задачи
Где – количество продуктов М и Н соответственно, – минимальная стоимость рациона откорма животных.
Система ограничений
Левая часть |
знак |
Правая часть |
200 |
>= |
200 |
14 |
<= |
14 |
Где имеют неотрицательные значения, а данная модель является линейной.
После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения
X1 |
X2 |
0,909091 |
0,318182 |
Целевая функция: |
2,159091 |
= = = => |
min |
Анализ результатов
Для того чтобы рацион был максимально дешевым, стоимостью 2,16$, необходимо приобрести 0,909кг продукта М и 0,318кг продукта Н.