Министерство образования и науки

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Ярославский государственный технический университет»

Кафедра «Высшей математики»

Проверил

к.п.н., доцент

кафедры ВМ

Е.Н. Трофимец

Оценка_______

«__» ___2012г.

Отчет № 1

по дисциплине: «Линейная алгебра»

тема: «Задачи линейного программирования»

Выполнил

студент гр.ЭМП-10

Юсубов.И.Э

«___» ______ 2012г.

_________

Ярославль 2012

Задача №1

Предприятие производит изделия трех видов, поставляет их заказчикам и реализует на рынке. Заказчикам требуется 1000 изделий первого вида, 2000 изделий второго вида и 2500 изделий третьего вида. Условия спроса на рынке ограничивают число изделий первого вида 2000 единицами, второго – 3000 и третьего – 5000 единицами. Для изготовления изделий используются 4 типа ресурсов. Количество ресурсов, потребляемых для производства одного изделия, общее количество ресурсов и прибыль от реализации одного изделия каждого вида заданы в табл.. Как организовать производство, чтобы:1) обеспечить заказчиков; 2) не допустить затоваривания; 4)получить максимальную прибыль?

Тип ресурсов	Вид изделий			Всего ресурсов
	1	2	3
1	500	300	1000		25000000
2	1000	200	100		30000000
3	150	300	200		20000000
4	100	200	400		40000000
Прибыль	20	40	50

Математическая модель задачи

Где 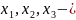число изделий первого, второго и третьего вида соответственно, а f- максимальная прибыль предприятия.

Система ограничений

левая часть	знак	правая часть
6900000	<=	25000000
3100000	<=	30000000
2200000	<=	20000000
2800000	<=	40000000

Где имеют неотрицательные значения, а данная модель является линейной

После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения

X1	X2	X3
2000	3000	5000

Целевая функция

410000

----->

max

Анализ результатов:

Для того чтобы получить максимальную прибыль в размере 41000, при этом обеспечить заказчиков и не допустить затоваривания рынка, необходимо произвести 2000 изделий первого вида, 3000 изделий второго вида и 5000 изделий третьего вида.

Задача № 2

Предприятие выпускает сливочное и шоколадное мороженое. Для изготовления мороженого используются молоко и наполнители, расходы которых на 1 кг мороженого приведены в табл.. Маркетинговые исследования показали, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого равна 46 руб, шоколадного – 48 руб. Какое количество мороженого каждого вида должно производиться, чтобы доход от его реализации был максимальным ?

Исходный продукт	Расход исходного продукта на 1 кг мороженого		Запас, кг
	Сливочное	Шоколадное
Молоко	0,8	0,5	400
Наполнители	0,4	0,8	365

Математическая модель задачи

Где необходимое количество сливочного и шоколадного мороженого соответственно, f- максимальное количество прибыли от реализации мороженого.

Система ограничений

левая часть	знак	правая часть
400	<=	400
365	<=	365
12,5	<=	100
300	<=	350

Где имеют неотрицательные значения, а данная модель является линейной.

После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения

X1	X2
312,5	300

Целевая функция

28775

---->

max

Анализ результатов

Для того чтобы получать максимальную прибыль в размере 28775 необходимо производить 312,5 кг сливочного и 300 кг шоколадного мороженого.

Задача № 3

Пусть собственные средства банка в сумме с депозитами составляет 100 млн. руб. Эти средства банк может разместить в кредиты по ставке r₁ и в государственные ценные бумаги по ставке r₂ . Так как кредиты менее ликвидны по сравнению с ценными бумагами, то r₁>r₂. Банк обязан не менее 35 % от суммы в 100 млн. руб. разместить в кредитах. Ликвидное ограничение состоит в том, что ценные бумаги должны составлять не менее 30 % средств размещенных в кредитах и ценных бумагах. Определить такое размещение средств в кредиты и ценные бумаги, при котором прибыль банка будет максимальной (r₁ =18%, r₂ =12%) .

Математическая модель задачи

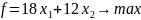
Где – необходимое количество кредитов и ценных бумаг соответственно, f – максимальное количество прибыли банка от размещения собственных средств.

Система ограничений

левая часть	знак	правая часть
50	<=	100
35	>=	35
15	>=	15

Где имеют неотрицательные значения, а данная модель является линейной.

После подставляем формулы в соответствующие ячейки MS Exсel и с помощью надстройки Поиск решения находим нужные значения

Х1	Х2
35	15

Целевая функция

810

---->

max

Анализ результатов

Для получения максимальной прибыли в размере 810 млн. руб. необходимо 35 млн.руб. собственных средств банка разместить в кредитах и 15 млн.руб. разместить в ценных бумагах.